题目内容
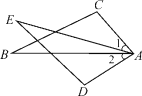
【题目】已知:△ABC≌△EDC.
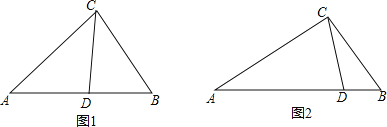
(1)若DE∥BC(如图1),判断△ABC的形状并说明理由.
(2)连结BE,交AC于F,点H是CE上的点,且CH=CF,连结DH交BE于K(如图2).求证:∠DKF=∠ACB

【答案】(1)△ABC是等腰三角形,理由见解析;(2)见解析;
【解析】
(1)根据全等三角形的性质和等腰三角形的判定解答即可;
(2)根据全等三角形的性质得出BC=CD,∠ACB=∠DCE,进而证明三角形全等解答即可.
(1)∵△ABC≌△EDC,
∴∠ABC=∠EDC,∠ACB=∠ECD,
∵DE∥BC,
∴∠EDC=∠ACB,
∴∠ABC=∠ACB,
∴AB=AC,
即△ABC是等腰三角形.
(2)∵△ABC≌△EDC,
∴BC=CD,∠ACB=∠DCE,
在△BCF和△DCH中,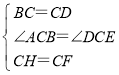 ,
,
∴△BCF≌△DCH,
∴∠FBC=∠HDC,
在△FBC和△FDK中,
∵∠FBC=∠HDC,∠BFC=∠DFK,
∴∠DKF=∠ACB.

练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
【题目】某市现在有两种用电收费方法:
分时电表 | 普通电表 | |
峰时(8:00~21:00) | 谷时(21:00到次日8:00) | |
电价0.55元/千瓦·时 | 电价0.35元/千瓦·时 | 电价0.52元/千瓦·时 |
小明家所在的小区用的电表都换成了分时电表.
解决问题:
(1)小明家庭某月用电总量为![]() 千瓦·时(
千瓦·时(![]() 为常数);谷时用电
为常数);谷时用电![]() 千瓦·时,峰时用电
千瓦·时,峰时用电![]() 千瓦·时,分时计价时总价为
千瓦·时,分时计价时总价为![]() 元,普通计价时总价为
元,普通计价时总价为![]() 元,求
元,求![]() ,
,![]() 与用电量的函数关系式.
与用电量的函数关系式.
(2)小明家庭使用分时电表是不是一定比普通电表合算呢?
(3)下表是路皓家最近两个月用电的收据:
谷时用电(千瓦·时) | 峰时用电(千瓦·时) |
181 | 239 |
根据上表,请问用分时电表是否合算?