��Ŀ����
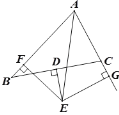
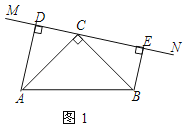
����Ŀ���ڡ�ABC�У���ACB=90�㣬AC=BC��ֱ��MN������C����AD��MN��D��BE��MN��E��
��1����ֱ��MN�Ƶ�C��ת��ͼ1��λ��ʱ
����˵����ADC�ա�CEB�����ɣ�
����˵��DE=AD+BE�����ɣ�
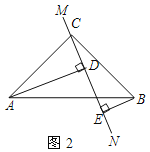
��2����ֱ��MN�Ƶ�C��ת��ͼ2��λ��ʱ��DE��AD��BE���������ĵ�����ϵ����ֱ���ں�����д�����������ϵ��__________��
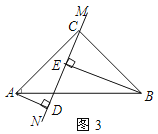
��3����ֱ��MN�Ƶ�C��ת��ͼ3��λ��ʱ��DE��AD��BE���������ĵ�����ϵ����ֱ���ں�����д�����������ϵ��__________��
���𰸡���1����֤������⣻��֤������⣻��2��DE=AD��BE����3��DE=BE��AD.
��������
��1���������������ACD+��BCE=90�㣬��DAC+��ACD=90�㣬����DAC=��BCE���ٸ���AAS���ɵ�֤��
�������õ�AD=CE��CD=BE�����ɵ�֤��
��2�����ƣ�1����֤�á�ACD=��EBC���Ƴ���ADC�ա�CEB����AD=CE��CD=BE��������֪���ɵô�𰸣�
��3��֤������ͬ��2��.
��1����֤������ͼ1�У�
��AD��DE��BE��DE��
���ADC=��BEC=90�㣬
�ߡ�ACB=90�㣬
���ACD+��BCE=90�㣬��DAC+��ACD=90�㣬
���DAC=��BCE��
����ADC����CEB��
 ��
��
���ADC�ա�CEB��AAS����
��֤��������֪��ADC�ա�CEB��
��AD=CE��CD=BE��
��DC+CE=DE��
��AD+BE=DE��
��2�����ۣ�DE=AD��BE��
����������
��ͼ2�У���BE��EC��AD��CE��
���ADC=��BEC=90�㣬
���EBC+��ECB=90�㣬
�ߡ�ACB=90�㣬
���ECB+��ACE=90�㣬
���ACD=��EBC��
�ڡ�ADC���CEB�У�
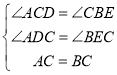 ��
��
���ADC�ա�CEB��AAS����
��AD=CE��CD=BE��
��DE=EC��CD=AD��BE��
��3�����ۣ�DE=BE��AD��
�������£���ͼ3�У��ߡ�ACB=90�㣬
���ACD+��BCE=90�㣬
�֡�AD��MN��BE��MN��
���ADC=��CED=90�㣬
���ACD+��DAC=90�㣬
���DAC=��ECB��
�ڡ�ACD���CBE�У�
 ��
��
���ACD�ա�CBE��AAS����
��AD=CE��CD=BE��
��DE=CD��CE=BE��AD.

����Ŀ��2019 �� 3 �� 31 �գ��Ͼ������µļ۸���ʽʵʩ��ʵ�������۽��Żݣ���ͨ����ÿ�³ֿ������������������ۼƽ����� 150 Ԫʱ��ÿ�γ���������Ʊ�۴� 9��5 �ۣ��������ۼƽ� ��� 150 Ԫʱ���ﵽ�涨�������ۼƽ�����ij˴Σ�Ʊ�������ۿ����±���ʾ��
�����ۼƽ�� | �ۿ� |
| 9�� |
| 8�� |
| 9.5�� |
С���ϡ��°�ÿ�γ����ĵ�������Ʊ��Ϊ 10Ԫ��2019�� 4�·����ϡ��°�ֿ��������� 40�Σ�
��1�������
��1 �� | ��2 �� | �� | ��15�� | ��16�� | ��17�� | �� | |
�����ۼ� ��Ԫ�� | 9.5 | 19 | �� | 142.5 | 152 | �� |
span>
��2��С�����µڼ��γ˳��������ۼƽ��� 20Ԫ������һԪһ�β���ʽ������⣩
��3��С�� 4�·��ϡ��°�ֿ����������������ۼƽ��Ϊ Ԫ��