��Ŀ����
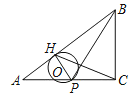
����Ŀ����ͼ������ABC�У���C��90����AB��10cm��BC��8cm����P�ӵ�A��ʼ������AC���C��2cm/s���ٶ��ƶ������ͬʱ����Q�ӵ�C��ʼ�ر�CB���B��1cm/s���ٶ��ƶ������P��Q�ֱ��A��Cͬʱ�������˶���ʱ��Ϊts������Q�˶�����Bʱ������ֹͣ�˶���

��1������P���߶�AC���˶�ʱ��P��C����֮��ľ����� ��cm�����ú�t�Ĵ���ʽ��ʾ��
��2�����˶��Ĺ����У��Ƿ����ijһʱ�̣�ʹ����PQC���������ABC�����![]() �������ڣ���t��ֵ���������ڣ�˵�����ɣ�
�������ڣ���t��ֵ���������ڣ�˵�����ɣ�
���𰸡���1����6��2t������2�����ڣ����ɼ�������t��4
��������
��1������AC��6cm��AP��2t�����ɵõ�������P���߶�AC���˶�ʱ��P��C����֮��ľ��루6��2t��cm��
��2���������������0��t��3ʱ����3��t��8ʱ���ֱ�������PQC���������ABC�����![]() ���з�����⼴�ɣ�
���з�����⼴�ɣ�
�⣺��1���ߡ�ABC�У���C��90����AB��10cm��BC��8cm��
���ɹ��ɶ�����AC��6cm��
�֡ߵ�P�ӵ�A��ʼ������AC���C��2cm/s���ٶ��ƶ���
��AP��2t��
�൱��P���߶�AC���˶�ʱ��P��C����֮��ľ��루6��2t��cm��
�ʴ�Ϊ����6��2t����
��2����ABC�����ΪS��ABC��![]() ��6��8��24��
��6��8��24��
�ٵ�0��t��3ʱ��PC��6��2t��QC��t��
��S��PCQ��![]() PC��QC��
PC��QC��![]() t��6��2t����
t��6��2t����
��![]() t��6��2t����4��
t��6��2t����4��
��t2��3t+4��0��
�ߡ���b2��4ac����7��0��
���һԪ���η�����ʵ������
��÷�Χ�²����ڣ�
�ڵ�3��t��8ʱ��PC��2t��6��QC��t��
��S��PCQ��![]() PC��QC��
PC��QC��![]() t��2t��6����
t��2t��6����
��![]() t��2t��6����4��
t��2t��6����4��
��t2��3t��4��0��
���t��4��1����ȥ����
�������������ڣ���t��4ʱ����PQC���������ABC�����![]() ��
��

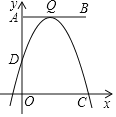
����Ŀ��ij��������һ����Ʒ���ɱ�ÿǧ��30Ԫ���涨ÿǧ���ۼ۲����ڳɱ����Ҳ�����70Ԫ�����г����飬ÿ���������y��ǧ�ˣ���ÿǧ���ۼ�x��Ԫ������һ�κ�����ϵ�������������±���
�ۼ�x��Ԫ/ǧ�ˣ� | 40 | 50 | 60 |
������y��ǧ�ˣ� | 100 | 80 | 60 |
��1����y��x֮��ĺ�������ʽ��
��2������Ʒÿ���������ΪW��Ԫ������W��x֮��ĺ�������ʽ������=�����ɱ�����
��3����˵����2����������W���ۼ�x�ı仯���仯���������ָ���ۼ�Ϊ����Ԫʱ������������������Ƕ��٣�