ΧβΡΩΡΎ»ί
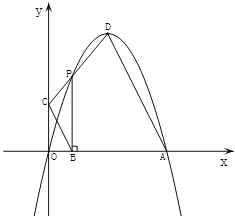
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§≈ΉΈοœΏyΘΫax2©¹4ax©¹![]() Θ®aΓΌ0Θ©ΫΜx÷α”ΎAΓΔBΝΫΒψΘ§ΫΜy÷α”ΎΒψCΘ§’βΧθ≈ΉΈοœΏΒΡΕΞΒψΈΣDΘ°
Θ®aΓΌ0Θ©ΫΜx÷α”ΎAΓΔBΝΫΒψΘ§ΫΜy÷α”ΎΒψCΘ§’βΧθ≈ΉΈοœΏΒΡΕΞΒψΈΣDΘ°
Θ®1Θ©«σΒψDΒΡΉχ±ξΘ°
Θ®2Θ©ΙΐΒψCΉςCEΓΈx÷αΫΜ≈ΉΈοœΏ”ΎΒψEΘ°Β±CEΘΫ2AB ±Θ§«σΒψDΒΡΉχ±ξΘ°
Θ®3Θ©’βΧθ≈ΉΈοœΏ”κ÷±œΏyΘΫ©¹xœύΫΜΘ§Τδ÷–“ΜΗωΫΜΒψΒΡΚαΉχ±ξΈΣ©¹1Θ°ΙΐΒψPΘ®mΘ§0Θ©Ήςx÷αΒΡ¥ΙœΏΘ§ΫΜ’βΧθ≈ΉΈοœΏ”ΎΒψMΘ§ΫΜ÷±œΏyΘΫ©¹x”ΎΒψNΘ§«“ΒψM‘ΎΒψNΒΡœ¬ΖΫΘ°Β±œΏΕΈMNΒΡ≥ΛΕ»ΥφmΒΡ‘ω¥σΕχ‘ω¥σ ±Θ§«σmΒΡ»Γ÷ΒΖΕΈßΘ°
Θ®4Θ©ΒψQ‘Ύ’βΧθ≈ΉΈοœΏ…œ‘ΥΕ·Θ§»τ‘Ύ’βΧθ≈ΉΈοœΏ…œ÷Μ¥φ‘ΎΝΫΗωΒψQΘ§¬ζΉψSΓςABQΘΫ3SΓςABCΘ§÷±Ϋ”–¥≥ωaΒΡ»Γ÷ΒΖΕΈßΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©(2Θ§©¹4a©¹![]() )ΘΜΘ®2Θ©(2Θ§
)ΘΜΘ®2Θ©(2Θ§![]() )ΘΜΘ®3Θ©©¹1ΘΦmΓή1ΘΜΘ®4Θ©0ΘΦaΘΦ
)ΘΜΘ®3Θ©©¹1ΘΦmΓή1ΘΜΘ®4Θ©0ΘΦaΘΦ![]() Μρ©¹
Μρ©¹![]() ΘΦaΘΦ©¹
ΘΦaΘΦ©¹![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΫΪyΘΫax2©¹4ax©¹![]() Μ·ΈΣΕΞΒψ ΫΦ¥Ω…–¥≥ωΒψDΒΡΉχ±ξΘΜ
Μ·ΈΣΕΞΒψ ΫΦ¥Ω…–¥≥ωΒψDΒΡΉχ±ξΘΜ
Θ®2Θ©”…Ε‘≥Τ÷αΖΫ≥ΧxΘΫ2ΦΑ≈ΉΈοœΏΒΡΕ‘≥Τ–‘Ω…ΆΤ≥ωCEΘ§ABΒΡ≥ΛΘ§ΆΤ≥ωΒψAΘ§BΒΡΉχ±ξΘ§ΫΪAΜρBΒΡΉχ±ξ¥ζ»κyΘΫax2©¹4ax©¹![]() ÷–Θ§Φ¥Ω…«σ≥ωaΒΡ÷ΒΘ§Ϋχ“Μ≤Ϋ–¥≥ωΒψDΒΡΉχ±ξΘΜ
÷–Θ§Φ¥Ω…«σ≥ωaΒΡ÷ΒΘ§Ϋχ“Μ≤Ϋ–¥≥ωΒψDΒΡΉχ±ξΘΜ
Θ®3Θ©œ»Α―xΘΫ-1¥ζ»κyΘΫ©¹x÷–Θ§«σ≥ωΫΜΒψΉχ±ξΘ§¥ζ»κyΘΫax2©¹4ax©¹![]() ÷–Θ§«σ≥ω≈ΉΈοœΏΫβΈω ΫΘ§”ΟΚ§mΒΡ¥ζ ΐ ΫΖ÷±π±μ Ψ≥ωMΘ§NΒΡΉχ±ξΘ§Ϋχ“Μ≤Ϋ±μ Ψ≥ωMNΒΡ≥ΛΕ»Θ§ΈΣΕΰ¥ΈΚ· ΐΘ§Ω…ΗυΨί‘ωΦθ–‘»ΖΕ®ΫαΙϊΘΜ
÷–Θ§«σ≥ω≈ΉΈοœΏΫβΈω ΫΘ§”ΟΚ§mΒΡ¥ζ ΐ ΫΖ÷±π±μ Ψ≥ωMΘ§NΒΡΉχ±ξΘ§Ϋχ“Μ≤Ϋ±μ Ψ≥ωMNΒΡ≥ΛΕ»Θ§ΈΣΕΰ¥ΈΚ· ΐΘ§Ω…ΗυΨί‘ωΦθ–‘»ΖΕ®ΫαΙϊΘΜ
Θ®4Θ©Ζ÷«ιΩωΧ÷¬έΘ§Β±aΘΨ0 ±ΚΆΒ±aΘΦ0 ±Θ§Ζ÷±πΝ–≥ω≤ΜΒ» ΫΜρ≤ΜΒ» ΫΉιΦ¥Ω…Θ°
Θ®1Θ©yΘΫax2©¹4ax©¹![]()
ΘΫaΘ®x©¹2Θ©2©¹4a©¹![]() Θ§
Θ§
ΓύΒψDΒΡΉχ±ξΈΣΘ®2Θ§©¹4a©¹![]() Θ©ΘΜ
Θ©ΘΜ
Θ®2Θ©ΓΏΕ‘≥Τ÷αΈΣ÷±œΏxΘΫ2Θ§CEΓΈx÷αΘ§
ΓύCEΘΫ4Θ°
ΓΏCEΘΫ2ABΘ§ΓύABΘΫ2Θ§
ΓύΒψAΓΔBΒΡΉχ±ξΈΣΘ®1Θ§0Θ©ΓΔΘ®3Θ§0Θ©Θ§
ΫΪΘ®1Θ§0Θ©¥ζ»κyΘΫax2©¹4ax©¹![]() ÷–Θ§
÷–Θ§
ΒΟΘ§a©¹4a©¹![]() ΘΫ0Θ§
ΘΫ0Θ§
ΫβΒΟΘ§aΘΫ©¹![]() Θ§
Θ§
Γύ©¹4a©¹![]() ΘΫ4ΓΝΘ®©¹
ΘΫ4ΓΝΘ®©¹![]() Θ©©¹
Θ©©¹![]() ΘΫ
ΘΫ![]() Θ§
Θ§
ΓύΒψDΒΡΉχ±ξΈΣΘ®2Θ§![]() Θ©ΘΜ
Θ©ΘΜ
Θ®3Θ©Α―xΘΫ-1¥ζ»κyΘΫ©¹x÷–Θ§ΒΟyΘΫ1Θ§
ΫΪΘ®©¹1Θ§1Θ©¥ζ»κyΘΫax2©¹4ax©¹![]() ÷–Θ§
÷–Θ§
ΒΟa+4a©¹![]() ΘΫ1Θ§
ΘΫ1Θ§
ΫβΒΟaΘΫ![]() Θ§
Θ§
ΓύyΘΫ![]() x2©¹2x©¹
x2©¹2x©¹![]() Θ§
Θ§
ΓύΒψMΘ§NΒΡΉχ±ξΖ÷±πΈΣΘ®mΘ§![]() m2©¹2m©¹
m2©¹2m©¹![]() Θ©Θ§Θ®mΘ§-mΘ©Θ§
ȩȧȮmȧ-mȩȧ
ΓύMNΘΫ©¹m©¹Θ®![]() m2©¹2m©¹
m2©¹2m©¹![]() Θ©ΘΫ©¹
Θ©ΘΫ©¹![]() m2+m+
m2+m+![]() Θ§
Θ§
ΓΏ©¹![]() ΘΦ0Θ§Ε‘≥Τ÷αΈΣ÷±œΏ
ΘΦ0Θ§Ε‘≥Τ÷αΈΣ÷±œΏ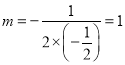 Θ§
Θ§
ΓύΒ±œΏΕΈMNΒΡ≥ΛΕ»ΥφmΒΡ‘ω¥σΕχ‘ω¥σ ±Θ§mΒΡ»Γ÷ΒΖΕΈß «©¹1ΘΦmΓή1ΘΜ
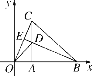
Θ®4Θ©ΔΌΒ±aΘΨ0 ±Θ§≈ΉΈοœΏΩΣΩΎΖΫœρœρ…œΘ§
ΒψCΉχ±ξΈΣΘ®0Θ§©¹![]() Θ©Θ§
Θ©Θ§
”…Θ®1Θ©÷ΣΘ§ΒψDΒΡΉίΉχ±ξΈΣ©¹4a©¹![]() Θ§
Θ§
Γύ”…Χβ“βΩ…Ν–Θ§©¹4a©¹![]() ΘΨ©¹
ΘΨ©¹![]() ΓΝ3Θ§
ΓΝ3Θ§
ΫβΒΟΘ§aΘΦ![]() Θ§
Θ§
Γύ0ΘΦaΘΦ![]() ΘΜ
ΘΜ
ΔΎΒ±aΘΦ0 ±Θ§≈ΉΈοœΏΩΣΩΎΖΫœρœρœ¬Θ§
ΒψCΉχ±ξΈΣΘ®0Θ§©¹![]() Θ©Θ§
Θ©Θ§
”…Θ®1Θ©÷ΣΘ§ΒψDΒΡΉίΉχ±ξΈΣ©¹4a©¹![]() Θ§
Θ§
Γύ”…Χβ“βΩ…Ν–Θ§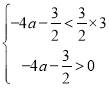 Θ§
Θ§
ΫβΒΟΘ§©¹![]() ΘΦaΘΦ
ΘΦaΘΦ![]() ΘΜ
ΘΜ
Ήέ…œΥυ ωΘ§aΒΡ»Γ÷ΒΖΕΈßΈΣ0ΘΦaΘΦ![]() Μρ©¹
Μρ©¹![]() ΘΦaΘΦ
ΘΦaΘΦ![]() Θ°
Θ°

 Ϋπ≈ΤΩΈΧΟΝΖœΒΝ–¥πΑΗ
Ϋπ≈ΤΩΈΧΟΝΖœΒΝ–¥πΑΗ »ΐ–¬Ωλ≥ΒΫπ≈Τ÷ή÷ήΝΖœΒΝ–¥πΑΗ
»ΐ–¬Ωλ≥ΒΫπ≈Τ÷ή÷ήΝΖœΒΝ–¥πΑΗ