题目内容
【题目】如图,菱形ABCD的边长是6,∠A=60°,E是AD的中点,F是AB边上一个动点,EG=EF且∠GEF=60°,则GB+GC的最小值是_____
【答案】![]()
【解析】
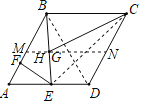
连接BD,由菱形的性质得到AB=AD,推出△ABD是等边三角形,得到BE⊥AD,取AB与CD的中点M,N,连接MN,点B关于MN的对称点是E,连接EC,此时CE的长就是GB+GC的最小值;求得HM=1.5,解直角三角形即可得到结论.
解:连接BD
∵四边形ABCD是菱形,
∴AB=AD,
∵∠A=60°,
∴△ABD是等边三角形,
∵E是AD的中点,
∴BE⊥AD,
取AB与CD的中点M,N,连接MN,
∴点B关于MN的对称点是E,连接EC,
此时CE的长就是GB+GC的最小值;
∵MN∥AD,
∴HM=![]() AE,
AE,
∵HB⊥HM,AB=6,∠A=60°,
∴MB=3,∠HMB=60°,
∴HM=1.5,
∴AE=3,
∵∠AEB=∠MHB=90°,
∴∠CBE=90°,
在Rt△EBC中,EB=3![]() ,BC=6,
,BC=6,
∴EC=3![]() ,
,
故答案为3![]() .
.

练习册系列答案
相关题目
【题目】二次函数![]() 为常数,
为常数,![]() 中的
中的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
x | -1 | 0 | 3 |
y | n | -3 | -3 |
当![]() 时,下列结论中一定正确的是________(填序号即可)
时,下列结论中一定正确的是________(填序号即可)
①![]() ;②当
;②当![]() 时,
时,![]() 的值随
的值随![]() 值的增大而增大;③
值的增大而增大;③![]() ;④当
;④当![]() 时,关于
时,关于![]() 的一元二次方程
的一元二次方程![]() 的解是
的解是![]() ,
,![]() .
.