题目内容
【题目】甲、乙两车分别从![]() 、
、![]() 两地同时出发,相向而行。甲车中途因故停车一段时间,之后以原速继续行驶到达目的地
两地同时出发,相向而行。甲车中途因故停车一段时间,之后以原速继续行驶到达目的地![]() ,此时乙车同时到达目的地
,此时乙车同时到达目的地![]() 。如图,是甲、乙两车离各自的出发地的路程
。如图,是甲、乙两车离各自的出发地的路程![]() 与时间
与时间![]() 的函数图像.
的函数图像.
(1)甲车的速度是多少![]() ,
,![]() 的值为多少;
的值为多少;
(2)求甲车在整个过程中,![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)直接写出甲、乙两车在途中相遇时![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)当
;(2)当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() (3)
(3)![]() .
.
【解析】
(1)根据题意和函数图象中的数据可以求得甲车的速度和a的值;
(2)根据函数图象中的数据可以求得甲车再次行驶过程中y与x之间的函数关系式,从而得到整个行驶过程中y与x的函数关系式;
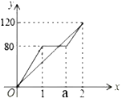
(3)由图可知A、B 两地的距离为120km,根据甲乙两车相遇时两车的路程和等于两地的距离分三种情况列出方程求解即可.
解:(1)由题意可得,
甲车的速度是:80÷1=80km/h,
a=1+(2-120÷80)=1.5;
(2)当0≤x≤1时,y=80x,
当1<x≤1.5时,y=80,
当1.5<x≤2时,设甲y与x之间的函数关系式是y=kx+b,
![]() ,
,
解得:![]() ,
,
所以y与x之间的函数关系式是y=80x-40.
综上,当0≤x≤1时,y=80x,当1<x≤1.5时,y=80,当1.5<x≤2时,y=80x-40;
(3)由图可知A、B 两地的距离为120km,
设乙车行驶过程中y与x之间的函数关系式是y=kx,
120=2k,得k=60,
∴乙车行驶过程中y与x之间的函数关系式是y=60x,
当0≤x≤1时,
∴80x+60x=120,
解得:x=![]() ;
;
当1<x≤1.5时,
80+60x=120,
解得:x=![]() (不符合题意,舍去);
(不符合题意,舍去);
当1.5<x≤2时,
80x-40+60x=120,
解得:x=![]() (不符合题意,舍去).
(不符合题意,舍去).
故甲、乙两车在途中相遇时x的值为![]() .
.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目