题目内容
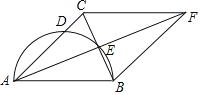
【题目】如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,其中∠ABC=∠AED=90°,CD与BE、AE分别交于点P、M.对于下列结论:①△CAM∽△DEM;②CD=2BE;③MPMD=MAME;④2CB2=CPCM.其中正确的是( )
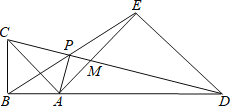
A. ①②B. ①②③C. ①②③④D. ①③④
【答案】D
【解析】
①求出∠CAM=∠DEM=90°,根据相似三角形的判定推出即可;
②求出△BAE∽△CAD,得出比例式,把AC=![]() AB代入,即可求出答案;
AB代入,即可求出答案;
③通过等积式倒推可知,证明△PME∽△AMD即可;
④2CB2转化为AC2,证明△ACP∽△MCA,问题可证.
∵在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,∠ABC=∠AED=90°,
∴∠BAC=45°,∠EAD=45°,
∴∠CAE=180°-45°-45°=90°,
即∠CAM=∠DEM=90°,
∵∠CMA=∠DME,
∴△CAM∽△DEM,故①正确;
由已知:AC=![]() AB,AD=
AB,AD=![]() AE,
AE,
∴![]() ,
,
∵∠BAC=∠EAD
∴∠BAE=∠CAD
∴△BAE∽△CAD,
∴![]() ,即
,即![]() ,即CD=
,即CD=![]() BE,故②错误;
BE,故②错误;
∵△BAE∽△CAD
∴∠BEA=∠CDA
∵∠PME=∠AMD
∴△PME∽△AMD
∴![]() ,
,
∴MPMD=MAME,故③正确;
由②MPMD=MAME
∠PMA=∠DME
∴△PMA∽△EMD
∴∠APD=∠AED=90°
∵∠CAE=180°-∠BAC-∠EAD=90°
∴△CAP∽△CMA
∴AC2=CPCM
∵AC=![]() AB,
AB,
∴2CB2=CPCM,故④正确;
即正确的为:①③④,
故选D.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目