题目内容
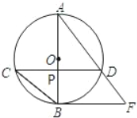
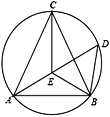
【题目】如图,在△ABC中,AC=BC,E是内心,AE的延长线交△ABC的外接圆于点D,以下四个结论:①BE=AE;②CE⊥AB;③△DEB是等腰三角形;④![]() .其中正确的个数是( )
.其中正确的个数是( )
A. 1个B. 2个C. 3个D. 4个
【答案】D
【解析】
根据E是内心,可得出∠CAD=∠BAD,则点D为弧BC的中点,又由AC=BC,得CE⊥AB;则延长BE交圆于一点也一定是弧AC的中点,则BE=AE;根据同弧所对的圆周角相等,得出三角形DEB与ABC三个角分别对应相等.则三角形DEB与ABC相似,从而得出第4个结论正确.
∵E是内心,∴∠CAD=∠BAD,∠CBE=∠EBA,
点D为弧BC的中点,
∵AC=BC,且CE为∠ACB的平分线,
∴CE⊥AB(三线合一),选项②正确;
∵AC=BC,∠ACE=∠BCE,CE=CE,
∴△ACE≌△BCE,(SAS)
∴∠CAE=∠CBE,
∴BE=AE,选项①正确;
∵∠CAD=∠BAD,
∴![]() ,
,
∴∠DBC=∠DAB,
∴∠EAB+∠EBA=∠DBC+∠EBC,即∠DEB=∠DBE,
∴DE=DB,
∴△DEB是等腰三角形,选项③正确;
∵△ABC和△BED都为等腰三角形,且两顶角∠ACB=∠EDB,
∴△ABC∽△BED,
∴![]() ,
,
∴![]() =
=![]() ,
,
∵DE=DB,BE=AE,
∴![]() ,选项④正确,
,选项④正确,
∴正确结论有4个.
故选:D.

【题目】蔬菜基地种植了娃娃菜和油菜两种蔬菜共![]() 亩,设种植娃娃菜
亩,设种植娃娃菜![]() 亩,总收益为
亩,总收益为![]() 万元,有关数据见下表:
万元,有关数据见下表:
成本(单位:万元/亩) | 销售额(单位:万元/亩) | |
娃娃菜 | 2.4 | 3 |
油菜 | 2 | 2.5 |
(1)求![]() 关于
关于![]() 的函数关系式(收益 = 销售额 – 成本);
的函数关系式(收益 = 销售额 – 成本);
(2)若计划投入的总成本不超过![]() 万元,要使获得的总收益最大,基地应种植娃娃菜和油菜各多少亩?
万元,要使获得的总收益最大,基地应种植娃娃菜和油菜各多少亩?
(3)已知娃娃菜每亩地需要化肥![]() kg,油菜每亩地需要化肥
kg,油菜每亩地需要化肥![]() kg,根据(2)中的种植亩数,基地计划运送所需全部化肥,为了提高效率,实际每次运送化肥的总量是原计划的
kg,根据(2)中的种植亩数,基地计划运送所需全部化肥,为了提高效率,实际每次运送化肥的总量是原计划的![]() 倍,结果运送完全部化肥的次数比原计划少
倍,结果运送完全部化肥的次数比原计划少![]() 次,求基地原计划每次运送多少化肥.
次,求基地原计划每次运送多少化肥.