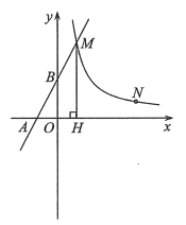
题目内容
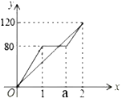
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,与反比例函数
两点,与反比例函数![]() 的图像交于点
的图像交于点![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() ,且
,且![]() ,点
,点![]() 在反比例函数
在反比例函数![]() 的图象上.
的图象上.
(1)求![]() 的值;
的值;
(2)在![]() 轴的正半轴上存在一点
轴的正半轴上存在一点![]() ,使得
,使得![]() 的值最小,求点
的值最小,求点![]() 的坐标;
的坐标;
(3)点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,把
,把![]() 向右平移
向右平移![]() 个单位到
个单位到![]() 的位置,当
的位置,当![]() 取得最小值时,请你在横线上直接写出
取得最小值时,请你在横线上直接写出![]() 的值,
的值,![]() .
.
【答案】(1)k = 4;(2)P的坐标为(![]() ,0);(3)4.75.
,0);(3)4.75.
【解析】
(1)运用平行线分线段成比例定理可得M点坐标,就可求k的值;
(2)找出N点的对称点N′,连接MN′与x轴交点就是点P;
(3)过点N′作x轴的平行线,取A关于这条平行线的对称点A′,连接A′B的直线经过N′,可求m的值.
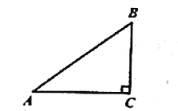
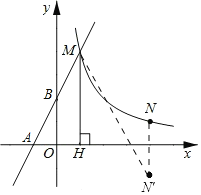
(1)把x=0代y=2x+2,得:y=2×0+2=2.∴点B(0,2),即BO=2,
∵BO∥MH,AB=BM,![]() ,
,
∴MH=2BO=4,
∵点M在y=2x+2上,
4+2x+2,x=1,
∴点M的坐标为(1,4),
∵M在反比例函y=![]() (x>0)的图象上,
(x>0)的图象上,
4=![]() ,k=4.
,k=4.
(2)如图所示,过点N作关于x轴的对称点N′,连接MN′,交x轴的正半轴于点P,则点P即为所求,此时PM+PN的值最小.
∵点N(a,1)是反比例函y=![]() (x>0)图象上的点,1=
(x>0)图象上的点,1=![]() ,a=4,
,a=4,
∴点N′的坐标为(4,-1),
设直线MN′的函数表达式y=kx+b,
![]() 解得
解得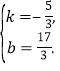
∴y=![]() x+
x+![]() ,
,
∴当y=0时,x=![]() ,即点P的坐标为(
,即点P的坐标为(![]() ,0).
,0).
(3)过点N′作x轴的平行线,取A关于这条平行线的对称点A′,连接A′B的直线经过N′
设A′B的解析式为:y=kx+b,
代入平移后的B(m,2)、A′(m-1,-2)
y=4x+2-4m
把N′(4,-1)代入,
解得:m=4.75.
故答案为:4.75.

 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案【题目】蔬菜基地种植了娃娃菜和油菜两种蔬菜共![]() 亩,设种植娃娃菜
亩,设种植娃娃菜![]() 亩,总收益为
亩,总收益为![]() 万元,有关数据见下表:
万元,有关数据见下表:
成本(单位:万元/亩) | 销售额(单位:万元/亩) | |
娃娃菜 | 2.4 | 3 |
油菜 | 2 | 2.5 |
(1)求![]() 关于
关于![]() 的函数关系式(收益 = 销售额 – 成本);
的函数关系式(收益 = 销售额 – 成本);
(2)若计划投入的总成本不超过![]() 万元,要使获得的总收益最大,基地应种植娃娃菜和油菜各多少亩?
万元,要使获得的总收益最大,基地应种植娃娃菜和油菜各多少亩?
(3)已知娃娃菜每亩地需要化肥![]() kg,油菜每亩地需要化肥
kg,油菜每亩地需要化肥![]() kg,根据(2)中的种植亩数,基地计划运送所需全部化肥,为了提高效率,实际每次运送化肥的总量是原计划的
kg,根据(2)中的种植亩数,基地计划运送所需全部化肥,为了提高效率,实际每次运送化肥的总量是原计划的![]() 倍,结果运送完全部化肥的次数比原计划少
倍,结果运送完全部化肥的次数比原计划少![]() 次,求基地原计划每次运送多少化肥.
次,求基地原计划每次运送多少化肥.