题目内容
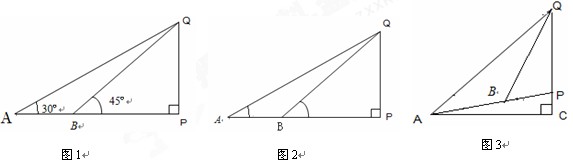
如图(1),在地面A、B两处测得地面上标杆PQ的仰角分别为30°、45°, 且测得AB=3米,求标杆PQ的长
(2)在数学学习中要注意基本模型的应用,如图(2),是测量不可达物体高度的基本模型:在地面A、B两处测得地面上标杆PQ的仰角分别为
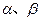 ,且测得AB=a米。
,且测得AB=a米。设PQ=h米,由PA-PB=a可得关于h的方程 ,解得h=
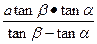
(3)请用上述基本模型解决下列问题:如图3,斜坡AP的倾斜角为15°,在A处测得Q的仰角为45°,要测量斜坡上标杆PQ的高度,沿着斜坡向上走10米到达B,在B处测得Q的仰角为60°,求标杆PQ的高。(结果可含三角函数)
(1)4.1米
(2)

(3)
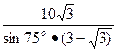
(1)设标杆PQ长为x米,
在RT△PAQ中,AP=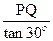
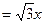 ,
,
在RT△PBQ中,BP=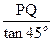 ="x" (1分)
="x" (1分)
由PA-PB=A B,得
B,得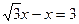 ,(2分)
,(2分)
解得x=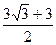 ≈ 4.1(3分)
≈ 4.1(3分)
答:标杆PQ的长约为4.1 米
(2) (5分)
(5分)
(3)过点Q作QD⊥AP于点D, (6分)
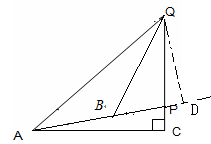
∠QAP=30o,∠QBP=45o,AB=10米,由(2)得,QD=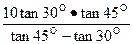 (7分)
(7分)
在RT△QPD中,∠QPD=75o,PQ=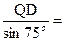
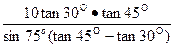
或PQ=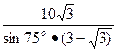
 (8分)
(8分)
在RT△PAQ中,AP=
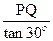
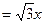 ,
, 在RT△PBQ中,BP=
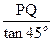 ="x" (1分)
="x" (1分)由PA-PB=A
 B,得
B,得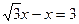 ,(2分)
,(2分)解得x=
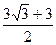 ≈ 4.1(3分)
≈ 4.1(3分)答:标杆PQ的长约为4.1 米
(2)
 (5分)
(5分)(3)过点Q作QD⊥AP于点D, (6分)

∠QAP=30o,∠QBP=45o,AB=10米,由(2)得,QD=
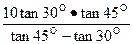 (7分)
(7分)在RT△QPD中,∠QPD=75o,PQ=
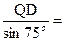
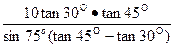
或PQ=
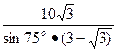
 (8分)
(8分)
练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
 、
、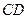 上有动点
上有动点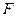 、
、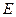 ,点
,点 的速度,在线段
的速度,在线段 的速度,在线段
的速度,在线段 ,求y 关于t的函数关系式,并写出函数定义域;
,求y 关于t的函数关系式,并写出函数定义域;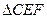 与
与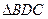 相似,求线段
相似,求线段 的长.
的长.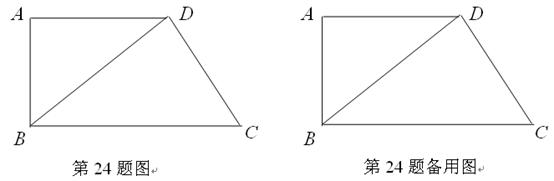
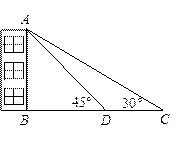
 ,金属丝就缩短0.002mm.把15℃的这种金属丝加热到50℃,再冷却降温到8℃,金属丝最后的长度比原来的长度伸长多少?
,金属丝就缩短0.002mm.把15℃的这种金属丝加热到50℃,再冷却降温到8℃,金属丝最后的长度比原来的长度伸长多少?