题目内容
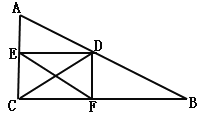
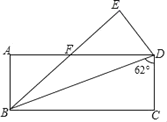
【题目】如图,将长方形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠DFE的度数为( )
A. 62°B. 56°C. 31°D. 28°
【答案】B
【解析】
先利用互余计算出∠FDB=28°,再根据平行线的性质得∠CBD=∠FDB=28°,接着根据折叠的性质得∠FBD=∠CBD=28°,然后利用三角形外角性质计算∠DFE的度数
∵四边形ABCD为矩形,
∴AD∥BC,∠ADC=90°,
∵∠FDB=90°∠BDC=90°62°=28°,
∵AD∥BC,
∴∠CBD=∠FDB=28°,
∵矩形ABCD沿对角线BD折叠,
∴∠FBD=∠CBD=28°,
∴∠DFE=∠FBD+∠FDB=28°+28°=56°.
故选:B

练习册系列答案
相关题目
【题目】“1285个服务站点”,“4.1万辆公共自行车”,“日均租骑量32.54万次”,“1小时内免费”,…,自2012年开通运营以来,太原公共自行车已经伴随太原市民走过近七个春秋.课外活动小组的同学们,在某双休日11:30-12:00对我市某个公共自行车服务站点的租骑量进行了观察记录.用“-6”表示骑走了6辆自行车,记录结果如下表(时间段不含前一时刻但含后一时刻,如11:30-11:35不含11:30但含11:35)
时间段 | 11:30-11:35 | 11:35-11:40 | 11:40-11:45 | 11:45-11:50 | 11:50-11:55 | 11:55-12:00 |
自行车数量 | -15 | +8 | -11 | +10 | -6 | +13 |
假设此服务站点在11:30时有自行车30辆,则在12:00时该站点有自行车( )

A.31辆B.30辆C.29辆D.27辆