Question

【题目】如图，△ABC中，∠ACB＝90°,∠B＝50°,△ABC绕点C顺时针旋转得到△A′B′C，点B′恰好落在线段AB上，AC、A′B′相交于O，则∠COA′的度数为_________．

Answer 1

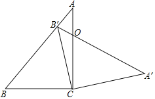
【答案】60°

【解析】

由三角形的内角和为180°可得出∠A=40°，由旋转的性质可得出BC=B′C，从而得出∠B=∠BB′C=50°，再依据三角形外角的性质结合角的计算即可得出结论．

解：∵在三角形ABC中，∠ACB＝90°，∠B＝50°，

∴∠A＝180°﹣∠ACB﹣∠B＝40°．

由旋转的性质可知：

BC＝B′C，

∴∠B＝∠BB′C＝50°．

又∵∠BB′C＝∠A+∠ACB′＝40°+∠ACB′，

∴∠ACB′＝10°，

∴∠COA′＝∠AOB′＝∠OB′C+∠ACB′＝∠B+∠ACB′＝60°．

故答案为：60°