题目内容
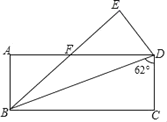
【题目】如图，二次函数y=ax2+bx+c的图象与x轴的交点A，B的横坐标分别为﹣1，3．与y轴负半轴交于点C，在下面四个结论中：①ac＜0；②2a﹣b=0；③a+b+c＞0；④c=﹣3a．其中正确的结论有（ ）
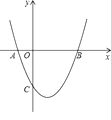
A. 1个 B. 2个 C. 3个 D. 4个
【答案】B
【解析】解：∵抛物线开口向上，∴a＞0．∵抛物线与y轴交点在y轴负半轴，∴c＜0，∴ac＜0，故①正确；
∵图象与x轴的交点A、B的横坐标分别为﹣1，3，∴对称轴为x=﹣
=
=1，∴b=﹣2a，∴2a+b=0，∴结论②不正确．
∵x=1时，y＜0，∴a+b+c＜0，∴结论③不正确．
∵点A的坐标为（﹣1，0），∴a﹣b+c=0．又∵b=﹣2a，∴a﹣（﹣2a）+c=0，∴c=﹣3a，∴结论④正确．
综上，可得正确的结论有两个：①④．
故选B．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
【题目】问题背景:
小红同学在学习过程中遇到这样一道计算题“计算4×2.112－4×2.11×2.22＋2.222”，她觉得太麻烦，估计应该有可以简化计算的方法，就去请教崔老师．崔老师说:你完成下面的问题后就可能知道该如何简化计算啦!
获取新知:
请你和小红一起完成崔老师提供的问题:
（1）填写下表:
x＝－1，y＝1 | x＝1，y＝0 | x＝3，y＝2 | x＝2，y＝－1 | x＝2，y＝3 | |
A＝2x－y | －3 | 2 | 4 | 5 | 1 |
B＝4x2－4xy＋y2 | 9 | 4 | 16 |
（2）观察表格，你发现A与B有什么关系?
解决问题:
（3）请利用A与B之间的关系计算:4×2.112－4×2.11×2.22＋2.222．
