Question

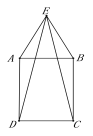
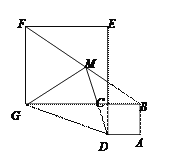
【题目】如图，正方形ABCD和正方形CEFG的面积分别为4 cm2,36cm2, 点G,C,B在一条直线上，M是BF的中点，则点M到GD的距离为_________cm．

Answer 1

【答案】

【解析】解：如图，作MK⊥DG于K，CN⊥DG于N，FH⊥DG于H，BT⊥DG于T．

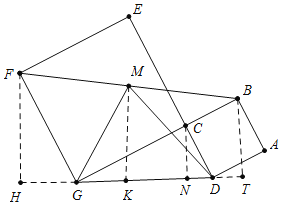
∵正方形ABCD和正方形CEFG的面积分别为4平方厘米和36平方厘米，∴FG=CG=6cm，CD=CB=2cm，∠FGC=∠GCD=∠H=∠CNG=90°，∴∠FGH+∠HFG=90°，∠FGH+∠CGN=90°，∴∠HFG=∠CGN．在△FGH和△GCN中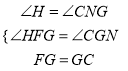， ，∴△FGH≌△GCN，∴FH=GN．在Rt△GCD中，DG==2cm，CN==cm，∴FH=GN===cm．∵CN∥BT，∴=，∴=，∴BT=cm．∵FM=MB，MK∥FH∥BT，∴KH=KT，∴MK==cm．

故答案为： ．