题目内容
【题目】如图,等边△ABC中,AD为BC边上的高,点M、N分别在AD、AC上,且AM=CN,连BM、BN,当BM+BN最小时,∠MBN=_____度.

【答案】30.
【解析】
如图1中,作CH⊥BC,使得CH=BC,连接NH,BH.证明△ABM≌△CHN(SAS),推出BM=HN,由BN+HN≥BH,可知B,N,H共线时,BM+BN=NH+BN的值最小,求出此时∠MBN即可解决问题.
解:如图1中,作CH⊥BC,使得CH=BC,连接NH,BH.
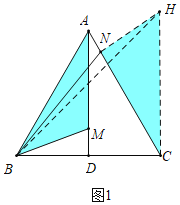
∵△ABC是等边三角形,AD⊥BC,CH⊥BC,
∴∠DAC=∠DAB=30°,AD∥CH,
∴∠HCN=∠CAD=∠BAM=30°,
∵AM=CN,AB=BC=CH,
∴△ABM≌△CHN(SAS),
∴BM=HN,
∵BN+HN≥BH,
∴B,N,H共线时,BM+BN=NH+BN的值最小,
如图2中,当B,N,H共线时,
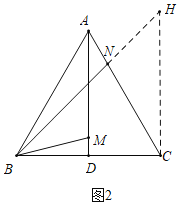
∵△ABM≌△CHN,
∴∠ABM=∠CHB=∠CBH=45°,
∵∠ABD=60°,
∴∠DBM=15°,
∴∠MBN=45°﹣15°=30°,
∴当BM+BN的值最小时,∠MBN=30°,
故答案为30.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


