题目内容
【题目】如图,在平面直角坐标系中,A(a,0)、B(0,b)、D(﹣d,d),连BD交x轴于E.
(1)如图1,若a、b、d满足(a﹣4)2+(a﹣b)2+![]() =0,求△ADE的面积.
=0,求△ADE的面积.
(2)如图2,在(1)的条件下,点P在x轴上A点右侧,连BP过点P作PQ⊥PB交直线AD于Q,求证:PQ=PB.
(3)如图3,设AB=c,且d=﹣2.当BD平分∠ABO时,试求a﹣b+c的值.

【答案】(1)![]() ;(2)详见解析;(3)4.
;(2)详见解析;(3)4.
【解析】
(1)作DC∥OA交y轴于C,根据非负数的性质分别求出a、b、d,根据相似三角形的性质求出OE,得到AE的长,根据三角形的面积公式计算即可;
(2)作DG⊥OA于G,连接BQ,根据圆周角定理得到∠QBP=∠QAP=45°,根据等腰三角形的判定定理证明;
(3)作DF⊥y轴于H,DH⊥x轴于H,DK⊥BA交BA的延长线于K,根据坐标与图形性质得到DF=DH=2,根据角平分线的性质得到DF=DK=2,得到DH=DK,证明Rt△DAH≌Rt△DAK,根据全等三角形的性质得到AK=AH=a﹣2,根据BK=BF列式计算,得到答案.
解:(1)∵(a﹣4)2+(a﹣b)2+![]() =0,
=0,
∴(a﹣4)2=0,(a﹣b)2=0,![]() =0,
=0,
∴a﹣4=0,a﹣b=0,d+2=0,
解得,a=b=4,d=﹣2,
如图1,作DC∥OA交y轴于C,
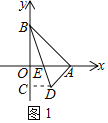
则△BOE∽△BCD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,OE=![]() ,
,
则AE=OA﹣OE=![]() ,
,
∴△ADE的面积=![]() ×
×![]() ×2=
×2=![]() ;
;
(2)如图2,作DG⊥OA于G,连接BQ,
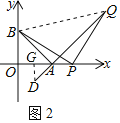
∵OA=OB,∠AOB=90°,
∴∠BAO=45°,
∵AG=OA﹣OG=2,
∴AG=DG,
∴∠DAG=45°,
∴∠BAQ=∠BAD=90°,∠QAP=∠DAG=45°,
∵∠BAQ=∠BPQ=90°,
∴点A、B、Q、P四点共圆,
∴∠QBP=∠QAP=45°,又∠BPQ=90°,
∴PQ=PB;
(3)作DF⊥y轴于H,DH⊥x轴于H,DK⊥BA交BA的延长线于K,
则DF=DH=2,
∵BD平分∠ABO,DF⊥y轴,DK⊥BA,
∴DF=DK=2,
∴DH=DK,BK=BF=b+2,
在Rt△DAH和Rt△DAK中,
![]() ,
,
∴Rt△DAH≌Rt△DAK(HL)
∴AK=AH=a﹣2,
∴BK=c+a﹣2,
∴c+a﹣2=b+2,
∴a﹣b+c=4.
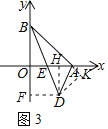

【题目】研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球.怎样估算不同颜色球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球试验.摸球试验的要求:先搅拌均匀,每次随机摸出一个球,放回盒中,再继续.
活动结果:摸球试验一共做了50次,统计结果如下表:
球的颜色 | 无记号 | 有记号 | ||
红色 | 黄色 | 红色 | 黄色 | |
摸到的次数 | 18 | 28 | 2 | 2 |
推测计算.由上述的摸球试验可推算:
(1)盒中红球、黄球各占总球数的百分比是多少?
(2)盒中有红球多少个?