ΧβΡΩΡΎ»ί
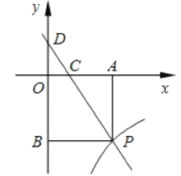
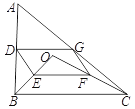
ΓΨΧβΡΩΓΩ»γΆΦΨΊ–ΈABCD÷–,AB=12,BC=8,EΓΔFΖ÷±πΈΣABΓΔCDΒΡ÷–Βψ,ΒψPΓΔQ¥”A. CΆ§ ±≥ωΖΔ,‘Ύ±ΏADΓΔCB…œ“‘ΟΩΟκ1ΗωΒΞΈΜœρDΓΔB‘ΥΕ·,‘ΥΕ· ±ΦδΈΣt(0<t<8).
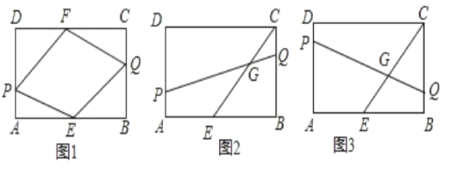
(1)»γΆΦ1Θ§Ν§Ϋ”PEΓΔEQΓΔQFΓΔPFΘ§«σ÷ΛΘΚΈό¬έt‘Ύ0<t<8ΡΎ»Γ»ΈΚΈ÷ΒΘ§ΥΡ±Ώ–ΈPEQFΉήΈΣΤΫ––ΥΡ±Ώ–ΈΘΜ
(2)»γΆΦ2Θ§Ν§Ϋ”PQΫΜCE”ΎGΘ§»τPG=4QGΘ§«σtΒΡ÷ΒΘΜ
(3)‘Ύ‘ΥΕ·Ιΐ≥Χ÷–Θ§ «Ζώ¥φ‘ΎΡ≥ ±ΩΧ ΙΒΟPQΓΆCE”ΎG?»τ¥φ‘ΎΘ§«κ«σ≥ωtΒΡ÷ΒΘΚ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…
ΓΨ¥πΑΗΓΩΘ®1Θ©ΦϊΫβΈωΘΜΘ®2Θ©![]() ΘΜΘ®3Θ©≤Μ¥φ‘ΎΘ§άμ”…ΦϊΫβΈω.
ΘΜΘ®3Θ©≤Μ¥φ‘ΎΘ§άμ”…ΦϊΫβΈω.
ΓΨΫβΈωΓΩ
Θ®1Θ©”…ΨΊ–ΈΒΡ–‘÷ ΒΟ≥ωCD=AB=12Θ§AD=BC=8Θ§ΓœA=ΓœB=ΓœC=ΓœD=90ΓψΘ§”…SAS÷ΛΟςΓςAPEΓ’ΓςCQFΘ§ΒΟ≥ωPE=QFΘ§Ά§άμΘΚPF=QEΘ§Φ¥Ω…ΒΟ≥ωΫα¬έΘΜ
Θ®2Θ©ΗυΨίΧβ“βΒΟΘΚAP=CQ=tΘ§ΓύPD=QB=8-tΘ§ΉςEFΓΈBCΫΜCD”ΎEΘ§ΫΜPQ”ΎHΘ§÷Λ≥ωEH «Χί–ΈABQPΒΡ÷–ΈΜœΏΘ§”…Χί–Έ÷–ΈΜœΏΕ®άμΒΟ≥ωEH=![]() Θ®AP+BQΘ©=4Θ§÷Λ≥ωGHΘΚGQ=3ΘΚ2Θ§”…ΤΫ––œΏΒΟ≥ωΓςEGHΓΉΓςCGQΘ§ΒΟ≥ωΕ‘”Π±Ώ≥…±»άΐ
Θ®AP+BQΘ©=4Θ§÷Λ≥ωGHΘΚGQ=3ΘΚ2Θ§”…ΤΫ––œΏΒΟ≥ωΓςEGHΓΉΓςCGQΘ§ΒΟ≥ωΕ‘”Π±Ώ≥…±»άΐ![]() Θ§Φ¥Ω…ΒΟ≥ωtΒΡ÷ΒΘΜ
Θ§Φ¥Ω…ΒΟ≥ωtΒΡ÷ΒΘΜ
Θ®3Θ©”…Ι¥Ι…Ε®άμ«σ≥ωCE=![]() =10Θ§ΉςEMΓΈBCΫΜPQ”ΎMΘ§”…Θ®2Θ©ΒΟΘΚME=4Θ§÷Λ≥ωΓςGCQΓΉΓςBCEΘ§ΒΟ≥ωΕ‘”Π±Ώ≥…±»άΐ«σ≥ωCG=t
=10Θ§ΉςEMΓΈBCΫΜPQ”ΎMΘ§”…Θ®2Θ©ΒΟΘΚME=4Θ§÷Λ≥ωΓςGCQΓΉΓςBCEΘ§ΒΟ≥ωΕ‘”Π±Ώ≥…±»άΐ«σ≥ωCG=t![]() Θ§ΒΟ≥ωEG=10-
Θ§ΒΟ≥ωEG=10-![]() tΘ§”…ΤΫ––œΏ÷ΛΟςΓςGMEΓΉΓςGQCΘ§ΒΟ≥ωΕ‘”Π±Ώ≥…±»άΐΘ§«σ≥ωt=0Μρt=8.5Θ§Φ¥Ω…ΒΟ≥ωΫα¬έΘ°
tΘ§”…ΤΫ––œΏ÷ΛΟςΓςGMEΓΉΓςGQCΘ§ΒΟ≥ωΕ‘”Π±Ώ≥…±»άΐΘ§«σ≥ωt=0Μρt=8.5Θ§Φ¥Ω…ΒΟ≥ωΫα¬έΘ°
(1)÷ΛΟςΘΚΓΏΥΡ±Ώ–ΈABCD «ΨΊ–ΈΘ§
ΓύCD=AB=12,AD=BC=8,ΓœA=ΓœB=ΓœC=ΓœD=90ΓψΘ§
ΓΏEΓΔFΖ÷±πΈΣABΓΔCDΒΡ÷–ΒψΘ§
ΓύAE=BE=6Θ§DF=CF=6Θ§
ΓύAE=BE=DF=CFΘ§
ΓΏΒψPΓΔQ¥”A. CΆ§ ±≥ωΖΔΘ§‘Ύ±ΏADΓΔCB…œ“‘ΟΩΟκ1ΗωΒΞΈΜœρDΓΔB‘ΥΕ·Θ§
ΓύAP=CQ=tΘ§
‘ΎΓςAPEΚΆΓςCQF÷–,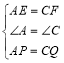 Θ§
Θ§
ΓύΓςAPEΓ’ΓςCQF(SAS),
ΓύPE=QFΘ§
Ά§άμΘΚPF=QEΘ§
ΓύΥΡ±Ώ–ΈPEQFΉήΈΣΤΫ––ΥΡ±Ώ–ΈΘΜ
(2)ΗυΨίΧβ“βΒΟΘΚAP=CQ=tΘ§
ΓύPD=QB=8tΘ§
ΉςEFΓΈBCΫΜCD”ΎEΘ§ΫΜPQ”ΎHΘ§»γΆΦ2Υυ ΨΘΚ
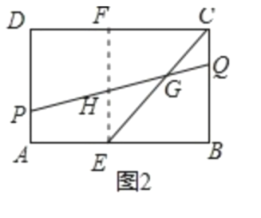
‘ρFΈΣCDΒΡ÷–ΒψΘ§HΈΣPQΒΡ÷–ΒψΘ§EF=BC=8Θ§
ΓύEH «Χί–ΈABQPΒΡ÷–ΈΜœΏΘ§
ΓύEH=![]() (AP+BQ)=4Θ§
(AP+BQ)=4Θ§
ÿPG=4QGȧ
ΓύGH:GQ=3:2Θ§
ÿEFøBCȧ
ΓύΓςEGHΓΉΓςCGQΘ§
Γύ![]() =
=![]() ,Φ¥4t=
,Φ¥4t=![]() Θ§
Θ§
ΫβΒΟΘΚt=![]() Θ§
Θ§
Γύ»τPG=4QG,tΒΡΈΣ![]() ÷Β;
÷Β;
(3)≤Μ¥φ‘ΎΘ§άμ”…»γœ¬ΘΚ
ΓΏΓœB=90ΓψΘ§BE=6Θ§BC=8Θ§
ΓύCE=![]() =10Θ§
=10Θ§
ΉςEMΓΈBCΫΜPQ”ΎMΘ§»γΆΦ3Υυ ΨΘΚ
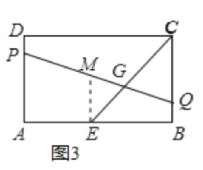
”…(2)ΒΟΘΚME=4Θ§
ÿPQâCEȧ
ΓύΓœCGQ=90Γψ=ΓœBΘ§
ΓΏΓœGCQ=ΓœBCEΘ§
ΓύΓςGCQΓΉΓςBCEΘ§
Γύ![]() ,Φ¥
,Φ¥![]() =
=![]() Θ§
Θ§
ΓύCG=![]() tΘ§
tȧ
ΓύEG=10![]() tΘ§
tȧ
ÿEMøBCȧ
ΓύΓςGMEΓΉΓςGQCΘ§
Γύ![]() ,Φ¥
,Φ¥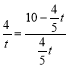 Θ§
Θ§
ΫβΒΟΘΚt=0Μρt=8.5Θ§
ΓΏ0<t<8Θ§
Γύ≤Μ¥φ‘ΎΓΘ

 ΐ―ßΑ¬»ϋ νΦΌΧλΧλΝΖΡœΨ©¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ
ΐ―ßΑ¬»ϋ νΦΌΧλΧλΝΖΡœΨ©¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ Ρœ¥σΫΧΗ®«άœ»Τπ≈ή νΦΌœΈΫ”ΫΧ≥ΧΡœΨ©¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ
Ρœ¥σΫΧΗ®«άœ»Τπ≈ή νΦΌœΈΫ”ΫΧ≥ΧΡœΨ©¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ