Question

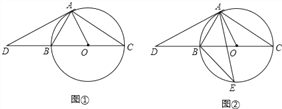
【题目】如图，点O是△ABC内一点，连结OB、OC，并将AB、OB、OC、AC的中点D、E、F、G依次连结，得到四边形DEFG．

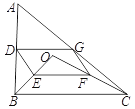
（）求证：四边形DEFG是平行四边形．

（）如果， ， ，求的长．

Answer 1

【答案】（1）见解析；（2）

【解析】试题分析：（1）根据三角形的中位线平行于第三边并且等于第三边的一半可得DG∥BC, ,EF∥BC, 从而得到DG∥EF，DG=EF，然后根据一组对边平行且相等的四边形是平行四边形证明即可；
（2）过点O作OM⊥BC于M,由含30°的直角三角形的性质和等腰直角三角形的性质求得结果．

试题解析：证明：∵AB、OB、OC、AC的中点分别为D. E. F.G，

∴DG∥BC, ,EF∥BC,

∴DG∥EF，DG=EF，

∴四边形DEFG是平行四边形；

(2)过点O作OM⊥BC于M,

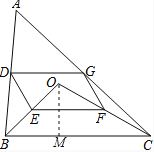
Rt△OCM中,

∴

∴

Rt△OBM中,

∴BM=OM=2，

∴

∴