题目内容
【题目】已知:如图,一次函数y=kx+3的图象与反比例函数y=![]() (x>0)的图象交于点P.PA⊥x轴于点A,PB⊥y轴于点B. 一次函数的图象分别交x轴、y轴于点C. 点D,且S△DBP=27,
(x>0)的图象交于点P.PA⊥x轴于点A,PB⊥y轴于点B. 一次函数的图象分别交x轴、y轴于点C. 点D,且S△DBP=27,![]()
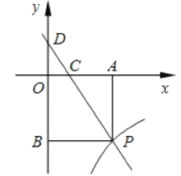
(1)求点D的坐标;
(2)求一次函数与反比例函数的解析式
【答案】(1)(0,3);(2)y=![]() x+3,y=
x+3,y=![]()
【解析】
(1)根据一次函数与y轴的交点,从而得出D点的坐标.
(2)根据在Rt△COD和Rt△CAP中,![]() ,OD=3,再根据S△DBP=27,从而得
,OD=3,再根据S△DBP=27,从而得
(1)∵一次函数y=kx+3与y轴相交,
∴令x=0,解得y=3,得D的坐标为(0,3);
(2)∵OD⊥OA,AP⊥OA,
∠DCO=∠ACP,
∠DOC=∠CAP=90°,
∴Rt△COD∽Rt△CAP,则![]() ,OD=3,
,OD=3,
∴AP=OB=6,
∴DB=OD+OB=9,
在Rt△DBP中,∴![]() =27,
=27,
即![]() ,
,
∴BP=6,故P(6,6),
把P坐标代入y=kx+3,得到k=![]() ,
,
则一次函数的解析式为:y=![]() x+3;
x+3;
把P坐标代入反比例函数解析式得m=36,
则反比例解析式为:y=![]() ;
;

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目