Question

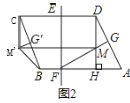
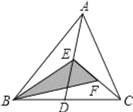
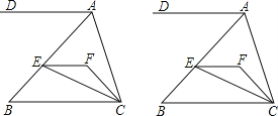
【题目】 如图，EF∥AD，AD∥BC，CE平分∠BCF，∠DAC=3∠BCF，∠ACF=20°．

（1）求∠FEC的度数；

（2）若∠BAC=3∠B，求证：AB⊥AC；

（3）当∠DAB=______度时，∠BAC=∠AEC．（请直接填出结果，不用证明）

Answer 1

【答案】（1）20°；（2）详见解析；（3）50

【解析】

（1）先根据CE平分∠BCF，设∠BCE=∠ECF=∠BCF=x．由∠DAC=3∠BCF可得出∠DAC=6x．根据AD∥EF，AD∥BC，得出EF∥BC，由平行线的性质即可得出x的值，进而得出结论；

（2）根据AD∥BC可知∠DAB=∠B，再由∠BAC=3∠B得出∠DAC=4∠B=120°，故∠B=30°，∠BAC=90°，由此可得出结论；

（3）根据（1）可得出∠BCF的度数，设∠BAD=∠B=α，由∠BAC=∠AEC即可得出结论．

解：（1）∵CE平分∠BCF，

∴设∠BCE=∠ECF=∠BCF=x．

∵∠DAC=3∠BCF，

∴∠DAC=6x．

∵AD∥BC，

∴∠DAC+∠ACB=180°，

∴6x+2x+20°=180°，

∴x=20°，即∠BCE=20°，

∵EF∥AD，AD∥BC，

∴EF∥BC，

∴∠BCE=∠FEC=20°；

（2）证明：∵AD∥BC，

∴∠DAB=∠B，

又∵∠BAC=3∠B，

∴∠DAC=4∠B，

由（1）可得∠BCA=20°×3=60°，

∴∠DAC=4∠B=120°，

∴∠B=30°，

∴∠BAC=30°×3=90°，

∴AB⊥AC；

（3）由（1）知∠BCE=20°，

∴∠BCF=40°．

∴∠DAC=3×40°=120°，

∵AD∥BC，

∴可设∠BAD=∠B=α，

∴∠AEC=∠B+∠BCE=α+20°，∠BAC=∠DAC-∠DAB=120°-α，

∴当∠BAC=∠AEC时，α+20°=120°-α，

解得α=50°，

∴∠DAB=50°．

故答案为：50．