Question

【题目】我市某乡镇在“精准扶贫”活动中销售一农产品，经分析发现月销售量y（万件）与月份x（月）的关系为：，每件产品的利润z（元）与月份x（月）的关系如下表：

x	1	2	3	4	5	6	7	8	9	10	11	12
z	19	18	17	16	15	14	13	12	11	10	10	10

（1）请你根据表格求出每件产品利润z（元）与月份x（月）的关系式；

（2）若月利润w（万元）=当月销售量y（万件）×当月每件产品的利润z（元），求月利润w（万元）与月份x（月）的关系式；

（3）当x为何值时，月利润w有最大值，最大值为多少？

Answer 1

【答案】（1）；（2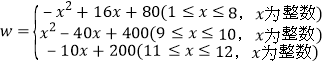）；（3）x=8时，w有最大值144万元.

【解析】（1）根据表格中的数据可以求得各段对应的函数解析式，本题得以解决；

（2）根据题目中的解析式和（1）中的解析式可以解答本题；

（3）根据（2）中的解析式可以求得各段的最大值，从而可以解答本题．

详解；（1）当1≤x≤9时，设每件产品利润z（元）与月份x（月）的关系式为z=kx+b，

，得，

即当1≤x≤9时，每件产品利润z（元）与月份x（月）的关系式为z=-x+20，

当10≤x≤12时，z=10，

由上可得，z=；

（2）当1≤x≤8时，w=（-x+20）（x+4）=-x2+16x+80

当9≤x≤10时，w=（-x+20）（-x+20）=x2-40x+400；

当11≤x≤12时，w=10（-x+20）=-10x+200；

∴w与x的关系式为： ；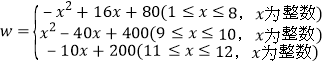

（3）当1≤x≤8时，w=-x2+16x+80=-（x-8）2+144，

∴当x=8时，w取得最大值，此时w=144；

当x=9时，w=121，

当10≤x≤12时，w=-10x+200，

则当x=10时，w取得最大值，此时w=100，

由上可得，当x为8时，月利润w有最大值，最大值144万元．