题目内容

【题目】如图，甲、乙两动点分别从正方形 ABCD 的顶点 A、C 同时沿正方形的边开始移动，甲点依顺时针方向环行，乙点依逆时针方向环行．若甲的速度是乙的速度的 3 倍，则它们第 2018 次相遇在边（ ）上．

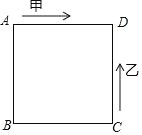
A. CDB. ADC. ABD. BC

【答案】B

【解析】

根据甲的速度是乙的速度的 3 倍，除第一次相遇路程和为两个边长外,其余每次相遇路程和都是四个边长，所以甲乙每隔四次循环一次，找到规律即可解题.

设正方形的边长为a,

∵甲的速度是乙的速度的 3 倍，

∴时间相同,甲乙的路程比是3:1,

∴第一次相遇,甲乙的路程和是2a,此时甲走了a, 乙走了a,在CD边相遇,

第二次相遇, 甲乙的路程和是4a,此时甲走了 ,乙走了,在AD边相遇,

第三次相遇, 甲乙的路程和是4a,此时甲走了 ,乙走了,在AB边相遇,

第四次相遇, 甲乙的路程和是4a,此时甲走了 ,乙走了,在BC边相遇,

第五次相遇, 甲乙的路程和是4a,此时甲走了 ,乙走了,在CD边相遇,

......

∵2018=5044+2,

∴它们第2018次相遇在边AD上,

故选B.

练习册系列答案
相关题目

【题目】（1）如图1，△ABC中，∠BAC=60°，内角∠ABC、∠ACB的平分线相交于点O，则∠BOC=______；

（2）如图2，△ABC中，∠BAC=60°，AD是△ABC的边BC上的高，且∠B=∠1，求∠C的度数．

【题目】△ABC是等边三角形，P为平面内的一个动点，BP=BA，0<∠PBC<180 ，DB平分∠PBC，且DB=DA．

（1）当BP与BA重合时（如图1），求∠BPD的度数；

（2）当BP在∠ABC的内部时(如图2)，求∠BPD的度数；

（3）当BP在∠ABC的外部时，请你直接写出∠BPD的度数.

【题目】已知将一矩形纸片ABCD折叠，使顶点A与C重合，折痕为EF．

（1）求证：CE=CF；

（2）若AB =8 cm，BC=16 cm，连接AF，写出求四边形AFCE面积的思路．

【题目】已知：如图，是由一个等边△ABE和一个矩形BCDE拼成的一个图形，其点B，C，D的坐标分别为(1，2)，(1，1)，(3，1)．

(1)直接写出E点和A点的坐标；

(2)试以点B为位似中心，作出位似图形A1B1C1D1E1，使所作的图形与原图形的位似比为3∶1；

(3)直接写出图形A1B1C1D1E1的面积．

【题目】如图1，在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E。

（1）①求证图1中△ADC≌△CEB；②证明DE=AD+BE；

（2）当直线MN绕点C旋转到图2的位置时，请说明DE=AD－BE的理由；

（3）当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE又具有怎样的等量关系?请直接写出这个等量关系（不必说明理由）。

【题目】下列各组条件中，能够判定△ABC≌△DEF 的是（ ）

A. ∠A＝∠D，∠B＝∠E，∠C＝∠FB. AB＝DE，BC＝EF，∠A＝∠D

C. ∠B＝∠E＝90°，BC＝EF，AC＝DFD. ∠A＝∠D，AB＝DF，∠B＝∠E

【题目】如图，在等腰△ABC中，，，F是AB边上的中点，点D、E分别在AC、BC边上运动，且保持,连接DE、DF、EF在此运动变化的过程中，下列结论：(1)是等腰直角三角形；四边形CDFE不可能为正方形，（3）长度的最小值为4；（4）连接CF，CF恰好把四边形CDFE的面积分成1：2两部分，则或其中正确的结论个数是

A. 1个B. 2个C. 3个D. 4个

【题目】 如图，EF∥AD，AD∥BC，CE平分∠BCF，∠DAC=3∠BCF，∠ACF=20°．

（1）求∠FEC的度数；

（2）若∠BAC=3∠B，求证：AB⊥AC；

（3）当∠DAB=______度时，∠BAC=∠AEC．（请直接填出结果，不用证明）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网