题目内容
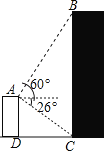
【题目】为了测量山坡上的电线杆PQ的高度,某数学活动小组的同学们带上自制的测倾器和皮尺来到山脚下,他们在A处测得信号塔顶端P的仰角是45°,信号塔底端点Q的仰角为30°,沿水平地面向前走100米到B处,测得信号塔顶端P的仰角是60°,求信号塔PQ得高度。
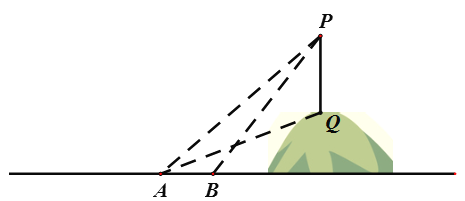
【答案】100米
【解析】
延长PQ交直线AB于点M,设PM的长为x米,先由三角函数得出方程求出PM,再由三角函数求出QM,相减得出PQ的长度即可.
解:延长PQ交直线AB于点M,如图所示:
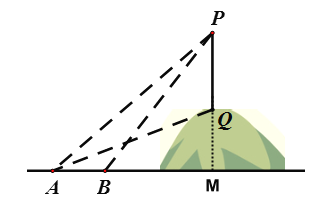
则∠PMA=90°,
设PM的长为x米,
在Rt△PAM中,∠PAM=45°,
∴AM=PM=x米,
∴BM=x100(米),
在Rt△PBM中,tan∠PBM=![]() ,
,
∴![]()
∴![]() ,
,
在Rt△QAM中,tan∠QAM=![]() ,
,
∴![]() ,
,
∴信号塔的高度![]() (米).
(米).
答:信号塔PQ的高度为100米.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】借鉴我们已有研究函数的经验,探索函数![]() 的图象与性质,探究过程如下,请补充完整.
的图象与性质,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() ,
,![]() ;
;
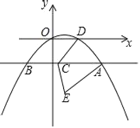
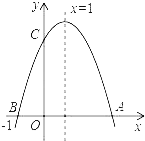
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出函数图象;
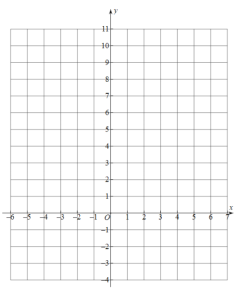
(3)观察函数图象:
①当方程![]() 有且仅有两个不相等的实数根,根据函数图象直接写出
有且仅有两个不相等的实数根,根据函数图象直接写出![]() 的取值范围为 ;
的取值范围为 ;
②在该平面直角坐标系中画出直线![]() 的图象,根据图象直接写出该直线与函数
的图象,根据图象直接写出该直线与函数![]()
![]() 的交点横坐标为: (结果保留一位小数).
的交点横坐标为: (结果保留一位小数).