题目内容
如图,用长为18m的篱笆(虚线部分),两面靠墙围成矩形的苗圃.
(1)设矩形的一边为x(m),面积为y(m2),求y关于x的函数关系式,并写出自变量x的取值范围;
(2)当x为何值时,所围苗圃的面积最大,最大面积是多少?
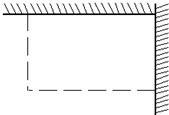
(1)设矩形的一边为x(m),面积为y(m2),求y关于x的函数关系式,并写出自变量x的取值范围;
(2)当x为何值时,所围苗圃的面积最大,最大面积是多少?

(1)由已知,矩形的另一边长为(18-x)m
则y=x(18-x)=-x2+18x
自变量x的取值范围是0<x<18.
(2)∵y=-x2+18x=-(x-9)2+81
∴当x=9时(0<9<18),苗圃的面积最大,最大面积是81m2.
又∵a=-1<0,y有最大值,
∴当x=-
=9时(0<x<18),
y最大值=
=81(m2).
则y=x(18-x)=-x2+18x
自变量x的取值范围是0<x<18.
(2)∵y=-x2+18x=-(x-9)2+81
∴当x=9时(0<9<18),苗圃的面积最大,最大面积是81m2.
又∵a=-1<0,y有最大值,
∴当x=-
| 18 |
| 2×(-1) |
y最大值=
| 0-182 |
| 4×(-1) |

练习册系列答案
相关题目