题目内容
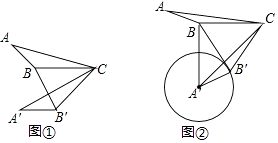
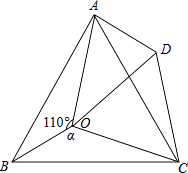
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD. 
(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由.
【答案】
(1)证明:∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴∠OCD=60°,CO=CD,
∴△OCD是等边三角形
(2)解:△AOD为直角三角形.
理由:∵△COD是等边三角形.
∴∠ODC=60°,
∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴∠ADC=∠BOC=α,
∴∠ADC=∠BOC=150°,
∴∠ADO=∠ADC﹣∠CDO=150°﹣60°=90°,于是△AOD是直角三角形.
【解析】(1)由旋转的性质可知CO=CD,∠OCD=60°,可判断:△COD是等边三角形;(2)由(1)可知∠COD=60°,当α=150°时,∠ADO=∠ADC﹣∠CDO,可判断△AOD为直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目