题目内容
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(3,0),B(0,4),则点B100的坐标为 . 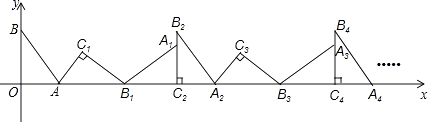
【答案】(600,4)
【解析】解:∵AO=3,BO=4,
∴AB=5,
∴OA+AB1+B1C2=3+5+4=12,
∴B2的横坐标为:12,且B2C2=4,
∴B4的横坐标为:2×12=24,
∴点B100的横坐标为:50×12=600.
∴点B100的纵坐标为:4.
故答案为:(600,4).
首先根据已知求出三角形三边长度,然后通过旋转发现,B、B2、B4…每偶数之间的B相差12个单位长度,根据这个规律可以求得B100的坐标.

练习册系列答案
相关题目