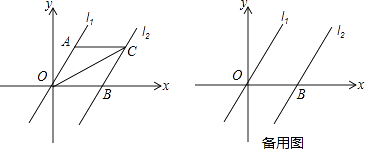题目内容
【题目】问题探究:如图①,四边形 ABCD是正方形,BE⊥BF,BE=BF,求证:△ABE≌△CBF;
方法拓展:如图②,ABCD是矩形,BC=2AB,BF⊥BE,BF=2BE,若矩形ABCD的面积为40,△ABE的面积为4,求阴影部分图形的面积.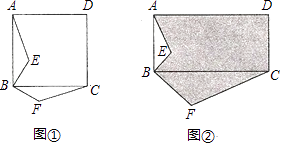
【答案】问题探究:
证明:如图①中,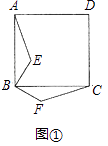
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∵BE⊥BF,BE=BF,
∴∠ABC=∠EBF=90°,
∴∠ABE=∠CBF,
在△ABE和△CBF中,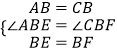 ,
,
∴△ABE≌△CBF,
方法拓展:
解:如图②中,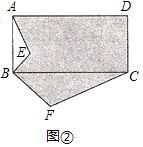
∵BC=2AB,BF=2BE,
∴ ![]() ,
,
∵∠ABE=∠CBF,
∴△ABE∽△CBF,![]() ,
,
∵S△ABE=4,
∴S△CBF=16,
∴S阴影部分图形=S矩形ABCD﹣S△ABE+S△CBF=40﹣4+16=52.
【解析】(1)根据两边夹角对应相等的两个三角形全等即可证明.(2)首先证明△ABE∽△CBF,求出△BFC的面积,根据S阴影部分图形=S矩形ABCD﹣S△ABE+S△CBF计算即可.
【考点精析】解答此题的关键在于理解相似三角形的性质的相关知识,掌握对应角相等,对应边成比例的两个三角形叫做相似三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目