题目内容
【题目】数学活动﹣旋转变换 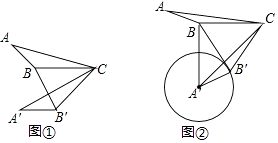
(1)如图①,在△ABC中,∠ABC=130°,将△ABC绕点C逆时针旋转50°,得到△A′B′C,连接BB′,求∠A′B′B的大小;
(2)如图②,在△ABC中,∠ABC=150°,AB=3,BC=5,将△ABC绕点C逆时针旋转60°得到△A′B′C,连接BB′,以A′为圆心,A′B′长为半径作圆. (Ⅰ)猜想:直线BB′与⊙A′的位置关系,并证明你的结论;
(Ⅱ)连接A′B,求线段A′B的长度.
【答案】
(1)解:由旋转变换的性质可知,∠A′B′C=∠ABC=130°,∠BCB′=50°,CB=CB′,
∴∠CB′B=65°,
∴∠A′B′B=∠A′B′C﹣∠CB′B=65°
(2)解:(Ⅰ)直线BB′与⊙A′相切,
∵∠A′B′C=∠ABC=150°,∠BCB′=60°,CB=CB′,
∴∠CB′B=60°,
∴∠A′B′B=∠A′B′C﹣∠CB′B=90°,
∴直线BB′与⊙A′相切;
(Ⅱ)在Rt△A′B′B中,∠A′B′B=90°,BB′=BC=5,AB′=AB=3,
由勾股定理得,A′B= ![]() =
= ![]()
【解析】(1)根据旋转变换的性质得到∠A′B′C=∠ABC=130°,∠BCB′=50°,CB=CB′,根据等腰三角形的性质求出∠A′B′B的大小;(2)(Ⅰ)根据旋转变换的性质求出∠A′B′B=90°,根据切线的判定定理证明;(Ⅱ)根据旋转变换的性质和勾股定理计算即可.
【考点精析】本题主要考查了直线与圆的三种位置关系和旋转的性质的相关知识点,需要掌握直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.

 名校课堂系列答案
名校课堂系列答案