Question

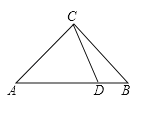
【题目】如图，抛物线与轴交于两点，与轴交于点连接，已知，且，

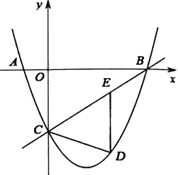
（1）求抛物线的解析式；

（2）若点为直线下方抛物线上一动点，过点作轴交于点，连接

①若，求此时点的坐标；

②若点关于直线的对称点恰好落在轴上，求此时点的坐标．

Answer 1

【答案】（1）y=x2x-3；（2）①点D坐标为（1，）或（3，-3）；②点D坐标为（，）．

【解析】

（1）设抛物线解析式为y=ax2+bx+c（a≠0），由C点坐标可得OC的长，根据可求出BC的长，利用勾股定理可求出OB的长，即可得出点B坐标，把A、B、C三点坐标代入y=ax2+bx+c，解方程组求出a、b、c的值即可得抛物线解析式；

（2）①由B、C坐标可求出直线BC的解析式，设D（m，m2m-3），把m代入直线BC解析式可得点E纵坐标，根据列方程求出m的值即可得答案；

②根据轴对称的性质可得∠E′CD=∠ECD，根据平行线的性质可得∠E′CD=∠CDE，即可得出∠ECD=∠CDE，可得DE=CE，设D（n，n2n-3），则E（n，n-3），根据两点间距离公式列方程求出n值即可得答案．

（1）设抛物线解析式为y=ax2+bx+c（a≠0），

∵C（0，-3），

∴OC=3，

∵，

∴BC==5，

∴OB==4，

∴B（4，0）

∵A（-1，0），

∴，

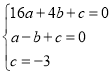解得：，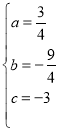

∴抛物线的解析式为y=x2x-3．

（2）设D（m，m2m-3），

设直线BC的解析式为y=kx+b，

∴，

解得：，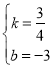

∴直线BC的解析式为y=x-3，

∵DE //ｙ轴，

∴点E坐标为（m，m-3），

∵，

∴m-3-（m2m-3）=，

解得：m1=1，m2=3，

当m=1时，m2m-3=，

当m=3时，m2m-3=-3，

∴点D坐标为（1，）或（3，-3）．

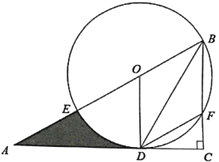
（3）如图，点关于直线的对称点恰好落在轴上，

∴∠E′CD=∠ECD，

∵DE//y轴，

∴∠E′CD=∠CDE，

∴∠ECD=∠CDE，

∴CE=DE，

设D（n，n2n-3），则E（n，n-3），

∵C（0，-3），

∴n-3-（n2n-3）==n，

解得：n1=，n2=0（舍去），

当n=时，n2n-3=，

∴点D坐标为（，）．