Question

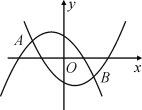
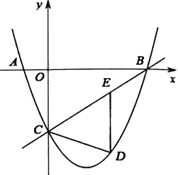
【题目】在平面直角坐标系中，抛物线与轴交于点和点．

（1）该抛物线的对称轴为直线________；

（2）已知该抛物线的开口向下，当时，的最大值是4，求此范围内的最小值．

（3）在（2）的条件下，直线过点，且与该抛物线的另一个交点为点，点为抛物线对称轴上的动点，当为等腰三角形时直接写出点的坐标．

Answer 1

【答案】（1）1；（2）最小值为－5；（3）点的坐标为(1，-3)或(1，)或(1，-)或(1，-5+)或(1，-5-)．

【解析】

（1）根据对称轴的公式，直接求解，即可；

（2）当时，的最大值是4，得n=4+m，把代入得：，求出m，n的值，由抛物线的对称性，可知：当x=4时，y有最小值，进而即可求解；

（3）先求出B，C的坐标，设P(1，t)，用含t的代数式表示出，，，分3种情况，分别列出关于t的方程，即可求解．

（1）抛物线的对称轴为：直线x=，

故答案是：1；

（2）∵该抛物线的开口向下，对称轴为：直线x=1，当时，的最大值是4，

∴当x=1时，的最大值=m-2m+n=4，即： n=4+m，

把代入，得：，

∴m=-1，n=3，

∴，

∵当时，4-1＞1-（-1），

∴当x=4时，y的最小值=，

答：此范围内的最小值为：-5；

（3）∵抛物线与轴交于点和点，对称轴为：直线x=1，

∴B(3，0)，

∵直线过点，

∴a=-3，

∴直线，

联立，得，解得：，

∴C(-2，-5)，

∵点为抛物线对称轴上的动点，

∴设P(1，t)，

则，，，

当PB=PC时，，解得：t=-3，即P(1，-3)，

当PB=BC时，，解得：t=，即P(1，)，P(1，-)，

当PC=BC时，，解得：t=-5，即P(1，-5+)，P(1，-5-)，

综上所述：点的坐标为：(1，-3)或(1，)或(1，-)或(1，-5+)或(1，-5-)．