题目内容
【题目】已知:在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 上一动点,以
上一动点,以![]() 为边,在
为边,在![]() 的右侧作等边
的右侧作等边![]() .
.
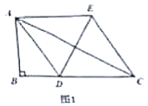

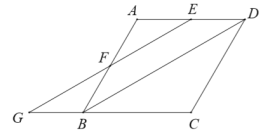
(1)当![]() 平分
平分![]() 时,如图1,四边形
时,如图1,四边形![]() 是________形;
是________形;
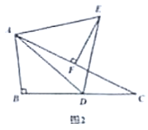
(2)过![]() 作
作![]() 于
于![]() ,如图2,求证:
,如图2,求证:![]() 为
为![]() 的中点;
的中点;
(3)若![]() .
.
①当![]() 为
为![]() 的中点时,过点
的中点时,过点![]() 作
作![]() 于
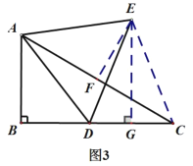
于![]() ,如图3,求
,如图3,求![]() 的长;
的长;
②点![]() 从
从![]() 点运动到
点运动到![]() 点,则点
点,则点![]() 所经过路径长为________(直接写出结果).
所经过路径长为________(直接写出结果).
【答案】(1)菱;(2)见解析;(3)①![]() ,②
,②![]()
【解析】
(1)根据角平分线的定义求出∠BAD=∠DAC=∠CAE=30°,进而得到AE∥BC,AE=AD=DC,根据菱形的判定定理可得结论;
(2)求出![]() ,证明
,证明![]() ,可得
,可得![]() ,根据
,根据![]() 可得结论;
可得结论;
(3)①过![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,首先证明
,首先证明![]() ,然后求出DG和AD的长,再利用勾股定理求出EG即可;②判断出点E的运动路径为EF,根据
,然后求出DG和AD的长,再利用勾股定理求出EG即可;②判断出点E的运动路径为EF,根据![]() 可得答案.
可得答案.
解:(1)∵![]() 是等边三角形,
是等边三角形,![]() 平分
平分![]() ,
,
∴∠BAD=∠DAC=∠CAE=30°,
∵![]() ,
,
∴AE∥BC,AD=DC,
∵AE=AD,
∴AE=DC,
∴四边形![]() 是平行四边形,
是平行四边形,
∵AD=DC,
∴四边形![]() 是菱形;
是菱形;
(2)∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() 为
为![]() 的中点;
的中点;
(3)①过![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,
,
∵![]() 为
为![]() 的中点,
的中点,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
在![]() 中,
中, ;
;
②由(2)可知,![]() ,
,
∴当点D从点B运动到点C时,点D的运动路径为BC,点E的运动路径为EF,
∵![]() ,
,
∴点![]() 从
从![]() 点运动到
点运动到![]() 点,则点
点,则点![]() 所经过路径长为
所经过路径长为![]() .
.

 全优点练单元计划系列答案
全优点练单元计划系列答案【题目】为庆祝建国70周年,某校举办了爱我中华知识竞赛活动.该校南、北两个校区七年级各有300名学生参加竞赛活动.为了解这两个校区参赛学生成绩情况,从中各随机抽取了10名学生的成绩进行调查,过程如下:
(收集、整理、描述数据)根据随机抽取的10名学生的成绩,制作了如下统计图表:
(说明:成绩90分及以上为优秀,80-89分为良好,60-79分为合格,60分以下为不合格)
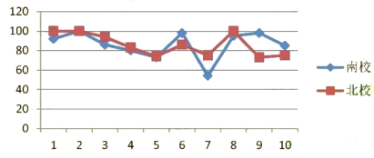
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
南校 | 92 | 100 | 86 | 80 | 73 | 98 | 54 | 95 | 98 | 85 |
北校 | 100 | 100 | 94 | 83 | 74 | 86 | 75 | 100 | 73 | 75 |
(分析数据)对上述数据进行分析,分别求出了两组样本数据的平均数、中位数、众数如下表:
校区 | 平均数(分) | 中位数(分) | 众数(分) |
南校 | 87 | 90.5 | |
北校 | 86 | 100 |
(得出结论)综合上述统计全过程,回答下列问题:
(1)补全表格.
(2)估计北校七年级学生竞赛成绩为优秀的人数.
(3)你认为哪个校区的七年级学生竞赛成绩比较好?说明你的理由.(从两个不同的角度说明推断的合理性)