Question

【题目】如图，点Ｏ是半径为3的圆形纸片的圆心，将这个圆形纸片按下列顺序折叠，使 和 都经过圆心Ｏ，则阴影部分面积是。

Answer 1

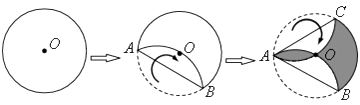
【答案】
【解析】如图，连接OC、OB、OA，

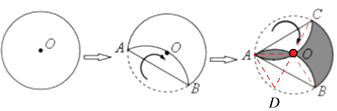
∵OA=OB=OC，

∴ ，

∴图中以A、B、O、C为端点的四个小弓形的面积相等，

∴S阴影=S扇形OBC，

过点O作OD⊥AB交 O于点D，则由折叠的性质可知：AD=AO，

∵AO=DO，

∴AO=AD=DO，

∴△AOD是等边三角形，

∴∠AOD=60°，则∠AOB=120°，

同理可得∠AOC=120°，

∴∠BOC=120°，

∴S阴影=S扇形OBC= .

【考点精析】本题主要考查了垂径定理和圆心角、弧、弦的关系的相关知识点，需要掌握垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等；在同圆或等圆中，同弧等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半才能正确解答此题．