题目内容
【题目】操作与探究
图(1)
定义:三边长和面积都是整数的三角形称为“整数三角形”.
数学学习小组的同学从32根等长的火柴棒(每根长度记为1个单位)中取出若干根,首尾依次相接组成三角形,进行探究活动.
小东用12根火柴棒,摆成如图所示的“整数三角形”;
小颖分用24根火柴棒摆出直角“整数三角形”;
小军受到小东、小颖的启发,用30根火柴棒摆出直角“整数三角形”;
(1)请你画出小颖和小军摆出的直角“整数三角形”的示意图;
(2)你能否也从中取出若干根,按下列要求摆出“整数三角形”,如果能,请画出示意图;如果不能,请说明理由.
①摆出一个等腰“整数三角形”;
②摆出一个非特殊(既非直角三角形,也非等腰三角形)“整数三角形”.
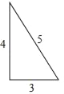
【答案】(1)小颖摆出直角“整数三角形”三边为6,8,10;小军摆出的直角“整数三角形”三边为5,12,13.(2)①详见解析;②详见解析.
【解析】
(1)利用勾股定理求出6,8,10和5,12,13符合要求,即可得出答案;
(2)要摆出等腰“整数三角形”,需保证三边长和面积都是整数,由三线合一可知,等腰三角形的一半是直角三角形,即画出直角三角形后再补充完整的等腰三角形;
(3)摆出一个非特殊“整数三角形”:要摆出“整数三角形”,需使三角形的底与高均为整数,可将两个直角三角形进行组合,常见的等高直角三角形有:6、8、10与8、15、17;9、12、15与5、12、13.
(1)如图1,
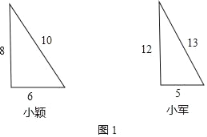
小颖摆出直角“整数三角形”三边为6,8,10;
小军摆出的直角“整数三角形”三边为5,12,13.
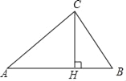
(2)摆出如图2所示三个不同的等腰“整数三角形”:
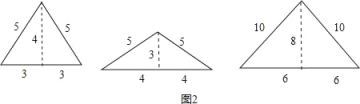
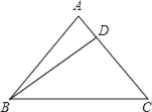
(3)摆出如图3所示一个非特殊“整数三角形”:

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目