题目内容
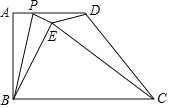
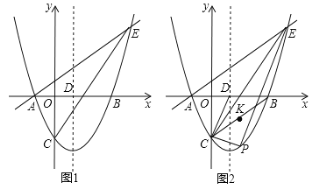
【题目】在△ACB和△DCE中,AB=AC,DE=DC,点E在AB上
(1)如图1,若∠ACB=∠DCE=60°,求证:∠DAC=∠EBC;
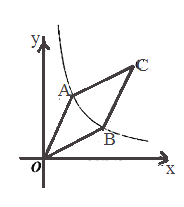
(2)如图2,设AC与DE交于点P.
①若∠ACB=∠DCE=45°,求证:AD∥CB;
②在①的条件下,设AC与DE交于点P,当tan∠ADE=![]() 时,直接写出
时,直接写出![]() 的值.
的值.
【答案】(1)见解析;(2)①见解析;②![]()
【解析】
(1)由等腰三角形的底角等于60°得出△ACB和△DCE都是等边三角形,再由“SAS”证得△DCA≌△ECB即可得出结论;
(2)①由等腰三角形的底角等于45°得出△ACB和△DCE都是等腰直角三角形,得出![]() 四点共圆,得到∠DAC=∠ACB=45°即可得出结论;
四点共圆,得到∠DAC=∠ACB=45°即可得出结论;
②作EH∥AD交AC于点H,则![]() ,由△ECB∽△DCA得
,由△ECB∽△DCA得![]() ,求得∠ADE=∠ACE,
,求得∠ADE=∠ACE,![]() ,可设AE=2m,则AC=4m,即BE=2m,
,可设AE=2m,则AC=4m,即BE=2m,
可得AD=![]() m,EH=2
m,EH=2![]() m,即可得出结果.
m,即可得出结果.
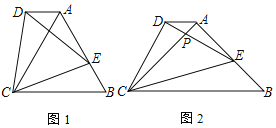
(1)证明:∵AB=AC,DE=DC,∠ACB=∠DCE=60°,
∴△ACB和△DCE都是等边三角形,
∴BC=AC,EC=DC,∠DCA=∠ECB,
在△DCA和△ECB中, ,
,
∴△DCA≌△ECB(SAS),
∴∠DAC=∠EBC;
(2)①证明:∵AB=AC,DE=DC,∠ACB=∠DEC=45°,
∴△ACB和△DCE都是等腰直角三角形,∠CAB=∠CAE=∠CDE=90°,
∴![]() 四点共圆,
四点共圆,
∴∠DAC=∠DEC=45,
∵∠ACB=∠DEC=45,
∴∠DAC=∠ACB=45°,
∴AD∥CB;
②解:作EH∥AD交AC于点H,如图2所示:
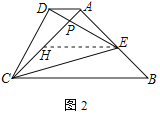
则:![]() ,
,
由①中的△ECB∽△DCA得:![]() ,
,
∵![]() 四点共圆,
四点共圆,
∴∠ADE=∠ACE,
∴![]() ,
,
设AE=2m,
∴![]() ,
,
∴AC=4m,
∴BE=AB﹣AE=AC﹣AE=4m﹣2m=2m,
∴AE=BE,
∴BC=![]() AC=4
AC=4![]() m,
m,
∵EH∥AD,AD∥CB,
∴EH∥CB,
∴EH是△ABC的中位线,
∴EH=![]() BC=
BC=![]() ×4
×4![]() m=2
m=2![]() m,
m,
![]() m,
m,
∴![]() =
=![]() =
=![]() .
.