Question

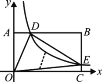
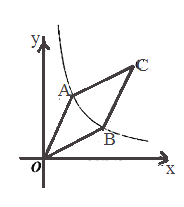
【题目】如图，面积为6的菱形AOBC的两点A，B在反比例函数（x>0）的图象上,则点C的坐标为___________.

Answer 1

【答案】（ ）

【解析】

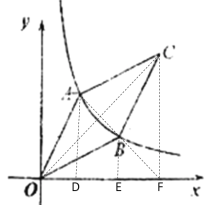
连接AB并延长交x轴于F，连接CF、OC，由菱形的对称性，反比例函数图象的对称性得到OC是第一象限的角平分线，进而得到∠COF=45, △OCF是等腰直角三角形，作AD⊥x轴，BE⊥x轴，根据k=4，菱形的面积是6，得到S梯形ADEB=3，设A()，由对称性得点B()，根据梯形面积公式得到，求得a的值即可证得点C的坐标.

连接AB并延长交x轴于F，连接CF、OC，

∵四边形AOBC是菱形，

∴点A、B关于直线OC对称，点O、C关于直线AB对称，OC⊥AB,

又∵点A、B在反比例函数的图象上，

∴OC是第一象限的角平分线，

∴∠COF=45,

∴∠AFO=∠COF=45,

∴CF⊥x轴，△OCF是等腰直角三角形，

作AD⊥x轴，BE⊥x轴，

∴S△AOD=S△BOE=2，

∵S△AOB=S菱形AOBC=3，

∴S梯形ADEB=3，

设A()，由对称性得点B()

∴

得： （不合题意，舍去），，

∴（负值舍去），

∴B（2，），

∴EF=BE=，

∴OF=CF=3，

∴C(),

故答案为：（）.