[题目]如图.在四边形ABCD中.AB∥CD.2AB=2BC=CD=10.tanB=.则AD= ．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，在四边形ABCD中，AB∥CD，2AB=2BC=CD=10，tanB=，则AD=______．

【答案】3

【解析】

过A作AF⊥CD于F，过C作CE⊥AB于E，根据矩形的性质得出AF=CE，AE=CF，求出AF和DF长，再根据勾股定理求出即可．

∵2AB=2BC=CD=10，

∴AB=BC=5，

过A作AF⊥CD于F，过C作CE⊥AB于E，

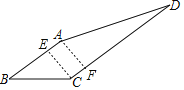
则∠AEC=∠AFD=∠BEC=90°，AF∥CE，

∵AB∥CD，

∴四边形AECF是矩形，

∴AE=CF，AF=CE，

∵在Rt△BEC中，tanB=，

又∵BC=5，

CE=3，BE=4，

∴AE=CF=5-4=1，AF=CE=3，

∵CD=10，

∴DF=10-1=9，

在Rt△AFD中，由勾股定理得：AD==3，

故答案为：．

练习册系列答案

【题目】如图1，在△ABC中，AC＝nAB，∠CAB＝α，点E，F分别在AB，AC上且EF∥BC，把△AEF绕点A顺时针旋转到如图2的位置．连接CF，BE．

（1）求证：∠ACF＝∠ABE；

（2）若点M，N分别是EF，BC的中点，当α＝90°时，求证：BE2+CF2＝4MN2；

（3）如图3，点M，N分别在EF，BC上且＝＝，若n＝，α＝135°，BE＝，直接写出MN的长．

【题目】如图，△ABC内接于⊙O，AB是⊙O的直径，过点A作AD平分∠BAC，交⊙O于点D，过点D作DE∥BC交AC的延长线于点E．

（1）依据题意，补全图形（尺规作图，保留痕迹）；

（2）判断并证明：直线DE与⊙O的位置关系；

（3）若AB=10，BC=8，求CE的长．

【题目】已知甲、乙两家公司员工日工资情况：甲公司日工资是底薪100元，每完成一件产品工资计3元；乙公司无底薪，40件以内（含40件）产品的部分每件产品工资计8元，超出40件的部分每件产品工资计10元，为此，在这两家公司各随机调查了100名工人日完成产品数，并整理得到如下频数分布表:

日完成产品数	38	39	40	41	42
甲公司工人数	20	40	20	10	10
乙公司工人数	10	20	20	40	10

（1）若甲、乙公司日工资加上其他福利，总的待遇相同，A、B两人分别到甲、乙公司应聘，都选中甲公司的概率是多少？

（2）试以这两家公司各100名工人日工资的平均数作为决策依据，若某人要去这两家公司应聘，为他做出选择，去哪一家公司的经济收入可能会多一些？

【题目】在△ACB和△DCE中，AB＝AC，DE＝DC，点E在AB上

（1）如图1，若∠ACB＝∠DCE＝60°，求证：∠DAC＝∠EBC；

（2）如图2，设AC与DE交于点P．

①若∠ACB＝∠DCE＝45°，求证：AD∥CB；

②在①的条件下，设AC与DE交于点P，当tan∠ADE＝时，直接写出的值．

【题目】如图，在平面直角坐标系中，A（﹣4，﹣2），B（﹣2，﹣2），C（﹣1，0）．

（1）将△ABC向右平移5个单位长度，画出平移后的△A1B1C1；

（2）将△ABC绕点C旋转180°，画出旋转后的△A2B2C，并直接写出点A运动的路径长；

（3）请直接写出△B1C1B2的外心的坐标．

【题目】如图，两个转盘中指针落在每个数字上的机会相等，现同时转动、两个转盘，停止后，指针各指向一个数字.小力和小明利用这两个转盘做游戏，若两数之积为非负数则小力胜；否则，小明胜.

（1）画树状图或列表求出各人获胜的概率。

（2）这个游戏公平吗？说说你的理由

【题目】端午节“赛龙舟，吃粽子”是中华民族的传统习俗．节日期间，小邱家包了三种不同馅的粽子，分别是：红枣粽子（记为A），豆沙粽子（记为B），肉粽子（记为C），这些粽子除了馅不同，其余均相同．粽子煮好后，小邱的妈妈给一个白盘中放入了两个红枣粽子，一个豆沙粽子和一个肉粽子；给一个花盘中放入了两个肉粽子，一个红枣粽子和一个豆沙粽子．

根据以上情况，请你回答下列问题：

（1）假设小邱从白盘中随机取一个粽子，恰好取到红枣粽子的概率是多少？

（2）若小邱先从白盘里的四个粽子中随机取一个粽子，再从花盘里的四个粽子中随机取一个粽子，请用列表法或画树状图的方法，求小邱取到的两个粽子中一个是红枣粽子、一个是豆沙粽子的概率．

试题分类