题目内容
【题目】如图,已知一次函数y1=ax+b的图象与x轴、y轴分别交于点D、C,与反比例函数y2=![]() 的图象交于A、B两点,且点A的坐标是(1,3)、点B的坐标是(3,m).
的图象交于A、B两点,且点A的坐标是(1,3)、点B的坐标是(3,m).
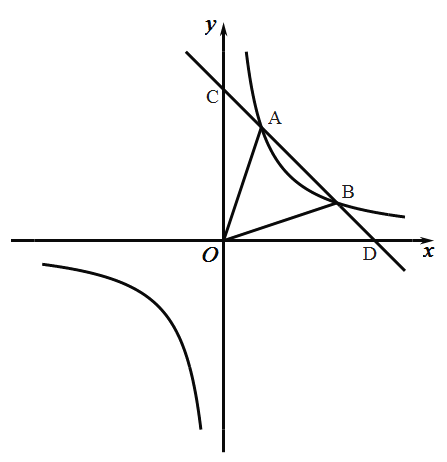
(1)求一次函数与反比例函数的解析式;
(2)求C、D两点的坐标,并求△AOB的面积;
(3)根据图象直接写出:当x在什么取值范围时,y1>y2?
【答案】(1)y2=![]() ,y1=﹣x+4;(2)4;(3)当 x 满足 1<x<3 、x<0时,则 y1>y2.
,y1=﹣x+4;(2)4;(3)当 x 满足 1<x<3 、x<0时,则 y1>y2.
【解析】
(1)把点A(1,3)代入y2=![]() ,求出k,得到反比例函数的解析式;再把B(3,m)代入反比例函数的解析式,求出m,得到点B的坐标,把A、B两点的坐标代入y1=ax+b,利用待定系数法求出一次函数的解析式;
,求出k,得到反比例函数的解析式;再把B(3,m)代入反比例函数的解析式,求出m,得到点B的坐标,把A、B两点的坐标代入y1=ax+b,利用待定系数法求出一次函数的解析式;
(2)把x=0代入一次函数解析式,求出y1=4,得到C点的坐标,把y1=0代入一次函数解析式,求出x=4,得到D点坐标,再根据S△AOB=S△AOD-S△BOD,列式计算即可;
(3)找出一次函数落在反比例函数图象上方的部分对应的自变量的取值即可.
解:(1)把点A(1,3)代入y2=![]() ,则3=
,则3=![]() ,即k=3,
,即k=3,
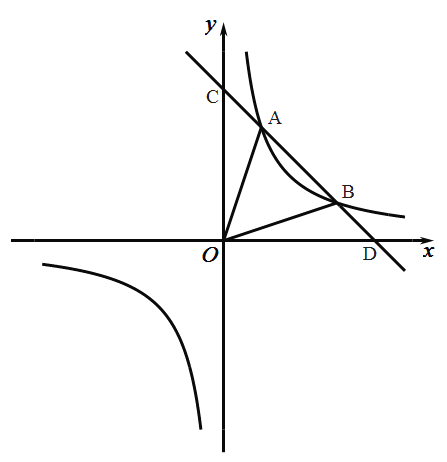
故反比例函数的解析式为:y2=![]() .
.
把点B的坐标是(3,m)代入y2=![]() ,得:m=
,得:m=![]() =1,
=1,
∴点B的坐标是(3,1).
把A(1,3),B(3,1)代入y1=ax+b,
得![]() ,解得
,解得![]() ,故一次函数的解析式为:y1=﹣x+4;
,故一次函数的解析式为:y1=﹣x+4;
(2)令x=0,则y1=4;令y1=0,则x=4,
∴C(0,4), D(4,0),
∴S△AOB=S△AOD﹣S△BOD=![]() ×4×3﹣
×4×3﹣![]() ×4×1=4;
×4×1=4;
(3)由图像可知x<0、1<x<3时,一次函数落在反比例函数图象上方,故满足y1>y2条件的自变量的取值范围: 1<x<3 、x<0.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目