ЬтФПФкШн
ЁОЬтФПЁП(1)ЗЂЯжЮЪЬт:ШчЭМЂйЦНааЫФБпаЮABЁЂCDЕФЖдНЧЯпЯрНЛгкЕуO,DEЁЮAC,CEЁЮBDЃЌПЩжЊ:ЫФБпаЮOCEDЪЧЪВУДаЮ(ВЛашвЊжЄУї).
(2)РрБШЬНОП:ШчЭМЂкОиаЮABCDЕФЖдНЧЯпЯрНЛгкЕуO,DEЁЮAC,CEЁЮBDЃЌЫФБпаЮOCEDЪЧЪВУДаЮ,ЧыЫЕУїРэгЩЃЛ
(3)ЭиеЙгІгУ:ШчЭМЂл,СтаЮABCDЕФЖдНЧЯпЯрНЛгкЕуO,ЁЯABC=60Ёу,BC=4,DEЁЮACНЛBCЕФбгГЄЯпгкЕуF,CEЁЮBDЧѓЫФБпаЮABFDЕФжмГЄ.
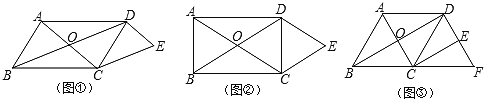
ЁОД№АИЁП(1)ЦНааЫФБпаЮЃЛЃЈ2ЃЉСтаЮЃЌжЄУїМћНтЮіЃЛЃЈ3ЃЉ20.
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУСНзщЖдБпЦНааЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉЯШХаЖЯГіЫФБпаЮOCEDЪЧЦНааЫФБпаЮЃЌдйгУОиаЮЕФаджЪМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЯШХаЖЯГіШ§НЧаЮCDFЪЧЕШБпШ§НЧаЮЃЌМДПЩЕУГіНсТлЃЎ
ЃЈ1ЃЉЁпDEЁЮACЃЌCEЁЮBD
ЁрЫФБпаЮOCEDЪЧЦНааЫФБпаЮЃЌ
ЙЪД№АИЮЊЃКЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉЫФБпаЮOCEDЪЧСтаЮЃЌ
жЄУїЃКЁпDEЁЮACЃЌCEЁЮBDЃЌ
ЁрЫФБпаЮOCEDЪЧЦНааЫФБпаЮЃЌ
ЁпЫФБпаЮABCDЪЧОиаЮЃЌ
ЁрOC=ODЃЌ
ЁрOCEDЪЧСтаЮЃЌ
ЙЪД№АИЮЊЃКСтаЮЃЎ
ЃЈ3ЃЉЁпADЁЮBCЃЌDEЁЮACЃЌ
ЁрЫФБпаЮACFDЪЧЦНааЫФБпаЮЃЌ
ЁпЫФБпаЮABCDЪЧСтаЮЃЌЁЯABC=60ЁуЃЌBC=4ЃЌ
ЁрAD=BC=AB=DC=4ЃЌЁЯDCF=60ЁуЃЌ
ЁрЁїDCFЪЧЕШБпШ§НЧаЮЃЌ
ЁрCF=DF=CD=4ЃЌ
ЁрЫФБпаЮABFDЕФжмГЄЮЊAB+BC+CF+DF+AD=4ЁС5=20ЃЎ