题目内容
【题目】综合题
（1）先解不等式组 
，然后判断 
是不是此不等式组的一个整数解．
（2）化简求值：先化简 
，再从1，2，3中选取一个适当的数代入求值．
【答案】
（1）解：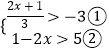 
由①得x＞﹣4
由②得x＜﹣2
∴原不等式的解集﹣4＜x＜﹣2
；
=1﹣3+1﹣4× 
=﹣3
∴﹣3 是不等式的整数解
（2）解：原式= 
= 
= 
∵a﹣2≠0，a+2≠0，
∴a≠±2，
∴当a=1时，原式=﹣3．
【解析】（1）先求得两个不等式的解集，然后依据同大取大；同小取小；大小小大中间找；大大小小找不到确定出不等式组的解集，接下来，化简x的值，最后，依据求得x的结果进行判断即可．
（2）先依据分式的减法和乘法法则进行计算，然后选取能够使得代数式有意义的x的值代入计算即可.
【考点精析】解答此题的关键在于理解零指数幂法则的相关知识，掌握零次幂和负整数指数幂的意义： a0=1（a≠0）;a-p=1/ap（a≠0，p为正整数），以及对整数指数幂的运算性质的理解，了解aman=am+n(m、n是正整数)；（am）n=amn(m、n是正整数)；(ab)n=anbn(n是正整数)；am/an=am-n(a不等于0，m、n为正整数）；（a/b）n=an/bn(n为正整数)．
备战中考寒假系列答案
【题目】为了调查学生对雾霾天气的了解程度，某校在学生中做了一次抽样调查，调查结果共分为四个等级：A．非常了解；B．比较了解；C．基本了解；D．不了解．根据调查统计结果，绘制了如图所示的不完整的三种统计图表．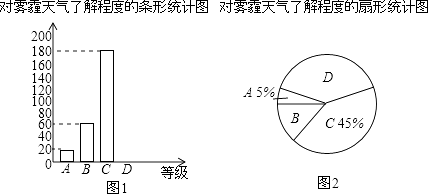
对雾霾的了解程度 | 百分比 |
A．非常了解 | 5% |
A．比较了解 | 15% |
C．基本了解 | 45% |
D．不了解 | n |
请结合统计图表，回答下列问题：
（1）本次参与调查的学生共有人，n=；扇形统计图中D部分扇形所对应的圆心角是度；
（2）请补全条形统计图；
（3）根据调查结果，学校准备开展关于雾霾的知识竞赛，某班要从“非常了解”程度的小明和小刚中选一人参加，现设计了如下游戏来确定，具体规则是：把四个完全相同的乒乓球标上数字1，2，3，4，然后放到一个不透明的袋中，一个人先从袋中随机摸出一个球，另一人再从剩下的三个球中随机摸出一个球．若摸出的两个球上的数字和为奇数，则小明去，否则小刚去．请用树状图或列表法说明这个游戏规则是否公平．
