Question

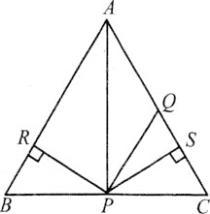
【题目】已知：如图，D是△ABC的边BC上的一点，且CD=AB，∠BDA=∠BAD，AE是△ABD的中线．

⑴若∠B=60°,求∠C的值；

⑵求证：AD是∠EAC的平分线．

Answer 1

【答案】（1）∠C=30°；（2）详见解析.

【解析】

（1）根据已知条件得到∠BAD=∠BDA=60°，于是得到AB=AD，等量代换得到CD=AD，根据等腰三角形的性质得到∠DAC=∠C，推出∠BDA=∠DAC+∠C=2∠C，即可得到结论；

（2）证明：延长AE到M，使EM=AE，连接DM，推出△ABE≌△MDE，根据全等三角形的性质得到∠B=∠MDE，AB=DM，根据全等三角形的判定定理得到△MAD≌△CAD，根据全等三角形的性质得到∠MAD=∠CAD于是得到结论．

（1）∵∠B=60°，∠BDA=∠BAD，

∴∠BAD=∠BDA=60°，

∴AB=AD，

∵CD=AB，

∴CD=AD，

∴∠DAC=∠C，

∴∠BDA=∠DAC+∠C=2∠C，

∵∠BAD=60°，

∴∠C=30°；

（2）证明：延长AE到M，使EM=AE，连接DM，

在△ABE和△MDE中，

，

∴△ABE≌△MDE，

∴∠B=∠MDE，AB=DM，

∵∠ADC=∠B+∠BAD=∠MDE+∠BDA=∠ADM，

在△MAD与△CAD，

，

∴△MAD≌△CAD，

∴∠MAD=∠CAD，

∴AD是∠EAC的平分线．