题目内容
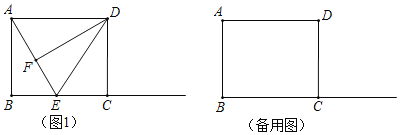
【题目】如图,![]() 中,
中,![]() ,
,![]() 垂直
垂直![]() 的角平分线于
的角平分线于![]() ,
,![]() 为
为![]() 的中点,则图中两个阴影部分面积之差的最大值为( )
的中点,则图中两个阴影部分面积之差的最大值为( )
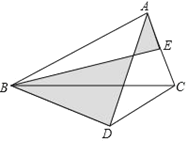
A.1.5B.3C.4.5D.9
【答案】C
【解析】
首先证明两个阴影部分面积之差=S△ADC,然后由DC⊥AC时,△ACD的面积最大求出结论即可.
延长BD交AC于点H.设AD交BE于点O.
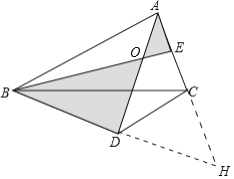
∵AD⊥BH,∴∠ADB=∠ADH=90°,∴∠ABD+∠BAD=90°,∠H+∠HAD=90°.
∵∠BAD=∠HAD,∴∠ABD=∠H,∴AB=AH.
∵AD⊥BH,∴BD=DH.
∵DC=CA,∴∠CDA=∠CAD.
∵∠CAD+∠H=90°,∠CDA+∠CDH=90°,∴∠CDH=∠H,∴CD=CH=AC.
∵BD=DH,AC=CH,∴S△CDH=![]() S△ADH
S△ADH![]() S△ABH.
S△ABH.
∵AE=EC,∴S△ABE![]() S△ABH,∴S△CDH=S△ABE.
S△ABH,∴S△CDH=S△ABE.
∵S△OBD﹣S△AOE=S△ADB﹣S△ABE=S△ADH﹣S△CDH=S△ACD.
∵AC=CD=3,∴当DC⊥AC时,△ACD的面积最大,最大面积为![]() 3×3
3×3![]() .
.
故选C.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
【题目】九(1)班组织班级联欢会,最后进入抽奖环节,每名同学都有一次抽奖机会,抽奖方案如下:将一副扑克牌中点数为“2”,“3”,“3”, “5”,“6”的四张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张牌点数后放回,完成一次抽奖,记每次抽出两张牌点数之差为x,按表格要求确定奖项.
奖项 | 一等奖 | 二等奖 | 三等奖 |
|x| | |x|=4 | |x|=3 | 1 |
(1)用列表或画树状图的方法求出甲同学获得一等奖的概率;
(2)求出每次抽奖获奖的概率?