题目内容
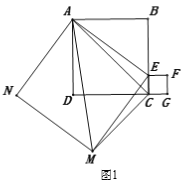
【题目】在矩形ABCD中,E为射线BC上一点,DF⊥AE于F,连接DE.
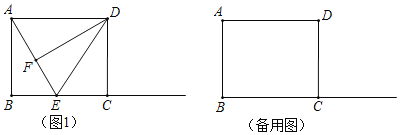
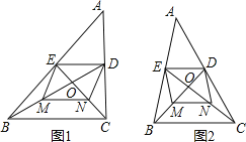
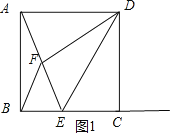
(1)如图1,若E在线段BC上,且CE=EF,求证:AD=AE;
(2)若AB=6,AD=10,在点E的运动过程中,连接BF.
①当△ABF是以AB为底的等腰三角形时,求BE的长;
②当BF∥DE时,若S△ADF=m,S△DCE=n,探究m﹣n的值并简要说明理由.
【答案】(1)见解析;(2)①BE的长是2或18;②m﹣n=0,理由见解析.
【解析】
(1)根据矩形的性质可证△CED≌△FED即可证明;
(2)①分两种情况:当点E在线段BC上时,AF=BF,利用矩形的性质解答即可;当点E在BC延长线上时,AF=BF,利用矩形的性质解答即可;
②当BF∥DE时,延长BF交AD于G,利用三角形的面积和平行四边形的面积之间的关系解答即可.
(1)∵四边形ABCD是矩形,
∴∠DCE=90°,AD∥BC,
∴∠ADE=∠DEC,
∵DF⊥AE
∴∠DCE=∠DFE=90°,
∵CE=EF,DE=DE,
∴△CED≌△FED(HL),
∴∠CED=∠FED,
∴∠ADE=∠AED,
∴AD=AE;
(2)①分两种情况:当点 E 在线段 BC 上时,AF=BF,如图 1 所示:
∴∠ABF=∠BAF,
∵∠ABF+∠EBF=90°,
∠BAF+∠BEF=90°,
∴∠EBF=∠BEF,
∴EF=BF,
∴AF=EF,
∵DF⊥AE,
∴DE=AD=10,
在矩形 ABCD 中,CD=AB=6,∠DCE=90°,
∴CE=8,
∴BE=10﹣8=2;
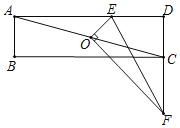
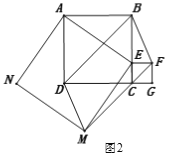
当点 E 在 BC 延长线上时,AF=BF,如图 2 所示:
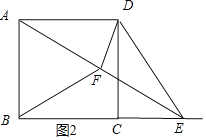
同理可证 AF=EF,
∵DF⊥AE,
∴DE=AD=10,
在矩形 ABCD 中,CD=AB=6,∠DCE=90°,
∴CE=8,
∴BE=10+8=18,
综上,BE的长是2或18;
②m﹣n=0,
理由如下:
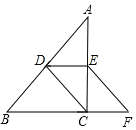
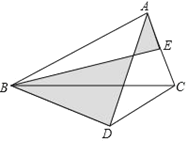
当 BF∥DE 时,延长 BF 交 AD 于 G.如图3:
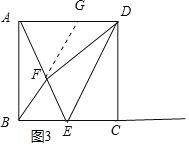
因为四边形ABCD是矩形,
∴AD∥BC,AD=BC,AB=CD,
∠BAG=∠DCE=90°,
∵BF∥DE,
∴四边形 BEDG 是平行四边形,
∴BE=DG,
∴S△DEF=![]() BEDG,AG=CE,
BEDG,AG=CE,
S△BEF+S△DFG=![]() SBEDG,
SBEDG,
∵△ABG≌△CDE,
∴S△ABG=S△CDE,
∵S△ABE=![]() SBEDG,
SBEDG,
∴S△ABE=S△BEF+S△DFG,
∴S△ABF=S△DFG,
∴S△ABF+S△AFG=S△DFG+S△AFG,
即S△ABG=S△ADF,
∴S△CDE=S△ADF,
即m﹣n=0.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案