题目内容
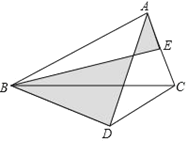
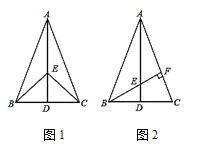
【题目】如图Rt△ABC,AB=CB,将△ABC绕A点旋转的度数为a(45°<a<180°),连接BD交AC于F,AH平分∠CAD交BD于点H,若△FHA为等腰三角形,则a=______.

【答案】135°或157.5°
【解析】
根据等腰直角三角形的性质得到∠BAC=45°,根据旋转的性质得到∠BAD=α,AB=AD,求得![]() ,根据角平分线的定义得到
,根据角平分线的定义得到![]() ,根据等腰三角形的性质得到
,根据等腰三角形的性质得到![]() ,求得
,求得![]() ,根据三角形的内角和列方程即可得到结论.
,根据三角形的内角和列方程即可得到结论.
∵△ABC是等腰直角三角形,
∴∠BAC=45°,
∵将△ABC绕A点旋转的度数为a得到△ADE,
∴∠BAD=α,AB=AD,
∴![]() ,
,
∵AH平分∠CAD交BD于点H,
∴![]() ,
,
∵AB=AD,
∴![]() ,
,
∴![]() ,
,
若△FHA为等腰三角形,
①当AF=AH,
∴![]() ,
,
∵∠FAH+∠AFH+∠AHF=180°,
∴![]() ,
,
解得:α=135°,
②当AF=FH时,
∴![]() ,
,
∵∠FAH+∠AFH+∠AHF=180°,
∴![]() ,
,
解得:α=180°,(不合题意,舍去);
③当AH=HF时,
∴∠HAF=∠HFA,
∴![]() ,
,
解得:![]() ,
,
综上所述,△FHA为等腰三角形,则a=135°或![]() ,
,
故答案为:135°或![]() .
.

练习册系列答案
相关题目