题目内容
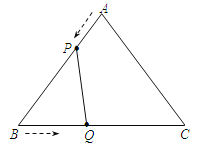
【题目】如图,在△ABC中,AB=AC=10厘米,BC=12厘米,点P从点A出发,沿AB边以1厘米/秒的速度向点B匀速移动;点Q从点B出发,沿BC边以2厘米/秒的速度向点C匀速移动.如果P、Q同时出发,当Q点到达C点时,P点随之停止运动.用t(秒)表示移动的时间(0≤t≤6).
(1)当PQ∥AC时,求t的值;
(2)当t为何值时,P、B、Q三点构成直角三角形.
【答案】(1)t=![]() ;(2)当t为
;(2)当t为![]() 秒或
秒或![]() 秒时,P、B、Q三点构成直角三角形
秒时,P、B、Q三点构成直角三角形
【解析】
(1)根据平行可以得到相似,然后根据相似三角形对应边的比等于相似比求得t值即可;
(2)分∠PQB=90°和∠QPB=90°两种情况分类讨论即可.
(1)∵PQ∥AC,∴△PBQ∽△ABC,∴![]() ,即
,即 ![]() ,解得:t=
,解得:t=![]() (秒);
(秒);
(2)过点A作AD⊥BC于D,如图1.
∵AB=AC,AD⊥BC,∴BD=DC=![]() BC=6.
BC=6.
∵∠B≠90°,∴P、B、Q三点构成直角三角形情况有两种:
①∠PQB=90°,即PQ∥AD,∴![]() ,即
,即 ![]() ,解得:t=
,解得:t=![]() (秒);
(秒);
②∠QPB=90°.而∠ADB=90°,∠B=∠B,∴△BPQ∽△BDA,∴![]() ,即
,即 ![]() ,解得:t=
,解得:t=![]() (秒);
(秒);
综上所述:当t为![]() 秒或
秒或![]() 秒时,P、B、Q三点构成直角三角形.
秒时,P、B、Q三点构成直角三角形.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目