题目内容
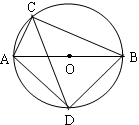
如图,⊙O的直径AB长为6,弦AC长为2,∠ACB的平分线交⊙O于点D,求四边形ADBC的面积.

9+4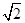
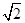
试题分析:先根据圆周角定理可得∠ACB=∠ADB=90°,在Rt△ABC中根据勾股定理求得BC的长,由根据角平分线的性质可得∠DAC=∠BCD,AD=DB,最后根据直角三角形的面积公式即可求得结果.
∵AB是直径,
∴∠ACB=∠ADB=90°
在Rt△ABC中,AB=6, AC= 2,
∴BC=
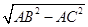 =
=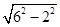 = 4
= 4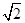
∵∠ACB的平分线交⊙O于点D
∴∠DAC=∠BCD
∴弧AD=弧BD
∴AD=BD
∴在Rt△ABD中,AD=BD=
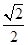 AB=3
AB=3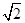
∴四边形ADBC的面积=S△ABC+S△ABD=
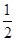 AC·BC+
AC·BC+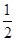 AD·BD=
AD·BD=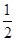 ×2×4
×2×4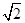 +
+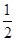 ×(3
×(3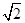 )2 =9+4
)2 =9+4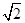 .
.点评:解答本题的关键是熟练掌握直径所对的圆周角是直角;在同圆或等圆中,相等的圆周角所对的弧和弦均相等.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目

 的直径CD与弦AB交于点M,添加一个条件 , 得到M是AB的中点。
的直径CD与弦AB交于点M,添加一个条件 , 得到M是AB的中点。
 是等腰三角形,
是等腰三角形,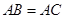 ,以
,以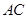 为直径的
为直径的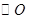 与
与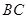 交于点
交于点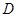 ,
,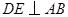 ,垂足为
,垂足为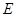 ,
,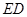 的延长线与
的延长线与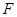 .
.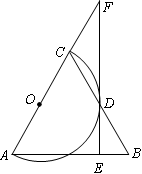
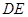 是
是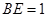 ,求
,求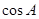 的值.
的值.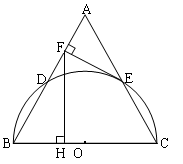

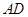 ∶
∶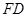 =1∶2,求⊙O的半径的长.
=1∶2,求⊙O的半径的长.