题目内容
【题目】如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.
(1)求证:∠ECD=∠EDC;
(2)若tanA= ![]() ,求DE长;
,求DE长;
(3)当∠A从15°增大到30°的过程中,求弦AD在圆内扫过的面积.
【答案】
(1)
证明:连结OD,
∵DE是⊙O的切线,∴∠EDC+∠ODA=90°,
又∵OA⊥OB,∴∠ACO+∠A=90°,
∵OA=OD,∴∠ODA=∠A,∴∠EDC=∠ACO,
又∵∠ECD=∠ACO,∴∠ECD=∠EDC.
(2)
解:∵tanA= ![]() ,∴
,∴ ![]() ,∴OC=2,
,∴OC=2,
设DE=x,∵∠ECD=∠EDC,∴CE=x,∴OE=2+x.
∵∠ODE=90°,∴OD2+DE2=OE2,
∴82+x 2=(2+x)2,x=15,∴DE=CE=15.
(3)
解:过点D作AO的垂线,交AO的延长于F,
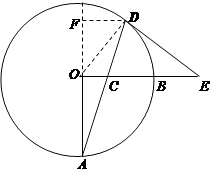
当 ![]() 时,则
时,则 ![]() ,DF=4,
,DF=4,
![]()
当 ![]() 时,
时, ![]() ,DF=4
,DF=4 ![]() ,
,
![]() ,
,
![]()
![]()
![]()
【解析】(1)运用切线的性质以及对顶角相等,角的等量代换可证得;(2)由tanA= ![]() ,可解出OC,由(1)得∠ECD=∠EDC , 等角对等边,则EC=DE,由勾股定理得OD2+DE2=OE2 , 构造方程解出DE的长;(3)分别求出
,可解出OC,由(1)得∠ECD=∠EDC , 等角对等边,则EC=DE,由勾股定理得OD2+DE2=OE2 , 构造方程解出DE的长;(3)分别求出 ![]() 和
和 ![]() 时,弓形ABD的面积,再用前者减去后者即可得到答案.
时,弓形ABD的面积,再用前者减去后者即可得到答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目







