题目内容
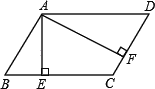
【题目】如图,在△ABC中,AB=![]() ,AC=
,AC=![]() ,BC=
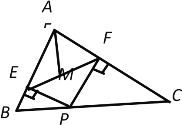
,BC=![]() ,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为__________.
,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为__________.
【答案】![]()
【解析】
根据勾股定理的逆定理可以证明∠BAC=90°;根据直角三角形斜边上的中线等于斜边的一半,则AM=![]() EF,要求AM的最小值,即求EF的最小值;根据三个角都是直角的四边形是矩形,得四边形AEPF是矩形,根据矩形的对角线相等,得EF=AP,则EF的最小值即为AP的最小值,根据垂线段最短,知:AP的最小值即等于直角三角形ABC斜边上的高.
EF,要求AM的最小值,即求EF的最小值;根据三个角都是直角的四边形是矩形,得四边形AEPF是矩形,根据矩形的对角线相等,得EF=AP,则EF的最小值即为AP的最小值,根据垂线段最短,知:AP的最小值即等于直角三角形ABC斜边上的高.
∵在△ABC中,AB=![]() ,AC=
,AC=![]() ,BC=
,BC=![]()
∴AB2+AC2=18+32=50=BC2
即∠BAC=90°.
又∵PE⊥AB于E,PF⊥AC于F,
∴四边形AEPF是矩形,
∴EF=AP.
∵M是EF的中点,
∴AM=![]() EF=
EF=![]() AP.
AP.
∵AP的最小值为AP⊥BC时,即为直角三角形ABC斜边上的高
∵![]()
∴AP=![]()
∴AM的最小值是![]()
故答案为:![]()

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
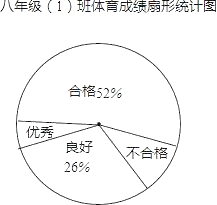
【题目】某校对九年级(1)班全体学生进行体育测试,测试成绩分为优秀、良好、合格和不合格四个等级,根据测试成绩绘制的不完整统计图表如下:
九年级(1)班体育成绩频数分布表:
等级 | 分值 | 频数 |
优秀 | 90﹣100分 | |
良好 | 75﹣89分 | 13 |
合格 | 60﹣74分 | |
不合格 | 0﹣59分 | 9 |
根据统计图表给出的信息,解答下列问题:
(1)九年级(1)班共有多少名学生?
(2)体育成绩为优秀的频数是 ,合格的频数为 ;
(3)若对该班体育成绩达到优秀程度的3个男生和2个女生中随机抽取2人参加学校体育竞赛,恰好抽到1个男生和1个女生的概率是 .