题目内容
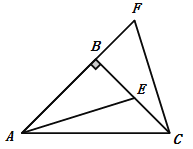
【题目】如图,在△ABC中,AB=BC, ∠ABC=90°,F为AB 延长线上的一点,点E在BC上,且AE=CF.
(1)求证: △ABE≌△CBF.
(2)若∠CAE=15°,求∠ACF的度数.
【答案】(1)证明见解析;(2)75°
【解析】试题分析:(1)根据“HL”即可判定:△ABE≌△CBF;
(2)由等腰直角三角形的性质得到∠BCA=45°,再由∠CAE=15°,得到∠BAE=30°,由全等三角形的性质得到∠BCF的度数,即可得到结论.
试题解析:(1)证明:∵∠ABC=90°,∴△ABE与△CBF为直角三角形.
在Rt△ABE与Rt△ BCF中,∵AB=BC,AE=CF,∴Rt△ABE≌Rt△ BCF;
(2) ∵ AB=BC, ∠ABC=90°,∴∠BCA=∠BAC=45°.
∵∠CAE=15°,∴∠BAE=30°.
∵△ABE≌△CBF,∴∠BCF=∠BAE=30°,∴∠ACF=75°.

练习册系列答案
相关题目
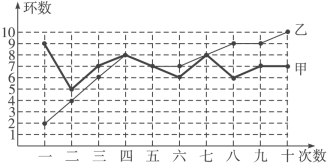
【题目】甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:
(1)请填写下表:
平均数 | 方差 | 中位数 | 命中9环及以上的次数 | |
甲 | 7 | 1.2 | 1 | |
乙 | 5.4 |
(2)请从下列四个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看;
②从平均数和中位数相结合看(分析谁的成绩好些);
③从平均数和命中9环以上的次数相结合看(分析谁的成绩好些);
④从折线图上两人射击命中环数的走势看(分析谁更有潜力).