题目内容
【题目】用加减消元法解下列方程
(1)![]() (2)
(2)![]()
(3)![]() (4)
(4)![]()
(5) ![]() (6)
(6) ![]()
【答案】(1)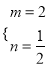 (2)
(2)![]() (3)
(3)![]() (4)
(4)![]() (5)
(5)![]() (6)
(6)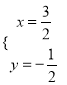
【解析】试题分析:(1)①和②相加即可得到m的值,再把m的值代入①即可求出n的值.
(2) ①和②相减即可得到x的值,再把x的值代入①即可求出y的值.
(3) ①和②相加即可得到y的值,再把y的值代入①即可求出x的值.
(4) ①和②相减即可得到y的值,再把y的值代入①即可求出x的值.
(5) ①×2减去②即可得到y的值,再把y的值代入①即可求出x的值.
(6) ①×2+②×5即可得到x的值,再把x的值代入①可求出y的值.
试题解析:
(1)![]()
①+②得,7m=14
解得m=2
把m=2代入①得3×2-2n=5
解得n=![]()
所以方程组的解是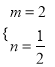 .
.
(2)![]()
①-②得2x=2
解得x=1
把x=1代入①得5×1+2y=7
解得y=1
所以方程组的解是![]() .
.
(3)![]()
①+②得,3y=-3
解得y=-1
把y=-1代入①得x+4×(-1)=-2
解得x=2
所以方程组的解是![]() .
.
(4) ![]()
①-②得,9y=-9
解得y=-1
把y=-1代入①得6x+5×(-1)=1
解得x=1
所以方程组的解是![]() .
.
(5) ![]()
①×2得4x-2y=2 ③
②+③得y=-1
把y=-1代入①得2x-(-1)=1
解得x=0
所以方程组的解是![]() .
.
(6) ![]()
①×2得6x-10y=14 ③
②×5得20x+10y=25 ④
③+④得26x=39
解得![]()
把![]() 代入①得3×
代入①得3×![]() -5y=7
-5y=7
解得![]()
所以方程组的解是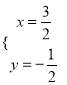 .
.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目