题目内容
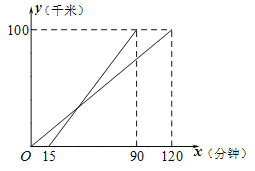
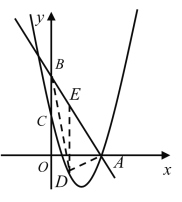
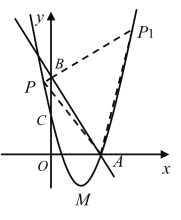
【题目】如图,直线![]() 分别与x轴,y轴交于点A,B两点,点C为OB的中点,抛物线
分别与x轴,y轴交于点A,B两点,点C为OB的中点,抛物线![]() 经过A,C两点.
经过A,C两点.

(1)求抛物线的函数表达式;
(2)点D是直线AB下方的抛物线上的一点,且![]() 的面积为
的面积为![]() ,求点D的坐标;
,求点D的坐标;
(3)点P为抛物线上一点,若![]() 是以AB为直角边的直角三角形,求点P到抛物线的对称轴的距离.
是以AB为直角边的直角三角形,求点P到抛物线的对称轴的距离.
【答案】(1)![]() ;(2)(2,-3);(3)
;(2)(2,-3);(3)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)由直线解析式求出A、B坐标,然后得出C点坐标,再用待定系数法求出抛物线解析式;
(2)过点D作DE⊥x轴,交直线AB于点E,设D(m,![]() ),利用S△ABD=
),利用S△ABD=![]() =
=![]() 得出方程,解出m值即可;
得出方程,解出m值即可;
(3)分点A是直角顶点和点B是直角顶点,结合图像,表示出△ABP三边长度,利用勾股定理得出方程,求解即可.
解:(1)直线![]() 中,
中,
令x=0,则y=10,令y=0,则x=5,
∴A(5,0),B(0,10),
∵点C是OB中点,
∴C(0,5),将A和C代入抛物线![]() 中,
中,
![]() ,解得:
,解得:![]() ,
,
∴抛物线表达式为:![]() ;
;
(2)联立:![]() ,
,
解得:![]() 或
或![]() ,
,
∴直线AB与抛物线交于点(-1,12)和(5,0),
∵点D是直线AB下方抛物线上的一点, 设D(m,![]() ),
),
∴-1<m<5,
过点D作DE⊥x轴,交直线AB于点E,
∴E(m,-2m+10),
∴DE=![]() =
=![]() ,
,
∴S△ABD=![]() =
=![]() =
=![]() ,
,
解得:m=2,
∴点D的坐标为(2,-3);
(3)抛物线表达式为:![]() ,
,
∵△APB是以AB为直角边的直角三角形,
设点P(n,![]() ),∵A(5,0),B(0,10),
),∵A(5,0),B(0,10),
∴AP2=![]() ,BP2=
,BP2=![]() ,AB2=125,
,AB2=125,
当点A为直角顶点时,
BP2= AB2+ AP2,
解得:n=![]() 或5(舍),
或5(舍),
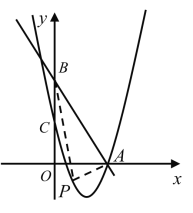
当点B为直角顶点时,
AP2= AB2+ BP2,
解得:n=![]() 或
或![]() ,
,
而抛物线对称轴为直线x=3,
则3-![]() =
=![]() ,
,![]() -3=
-3=![]() ,3-
,3-![]() =
=![]() ,
,
综上:点P到抛物线对称轴的距离为:![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目